
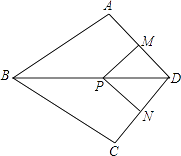
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N. 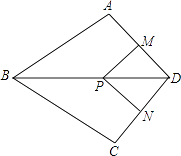
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
【答案】
(1)证明:∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
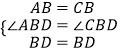 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB
(2)证明:∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
【解析】(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.


科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线l1经过点(1,﹣3)和(3,1),直线l2经过(1,0),且与直线l1交于点A(2,a).
(1)求a的值;
(2)A(2,a)可看成怎样的二元一次方程组的解?
(3)设直线l1与y轴交于点B,直线l2与y轴交于点C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果用﹣10%表示某商品的出口额比上一年减少10%,那么+12%则表示该商品的出口额比上一年( )
A.减少12%
B.增加12%
C.减少22%
D.增加2%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com