
【题目】如图所示,已知△ABC和△DCE均是等边三角形,点B. C. E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论中:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC,正确的是( )个

A.1B.2C.3D.4
【答案】D
【解析】
首先根据等边三角形的性质,得到BC=AC,CD=CE,∠ACB=∠BCD=60°,然后由SAS判定△BCD≌△ACE,根据全等三角形的对应边相等即可证得①正确;又由全等三角形的对应角相等,得到∠CBD=∠CAE,根据ASA,证得△BCF≌△ACG,即可得到②正确,同理证得CF=CG,得到△CFG是等边三角形,易得③正确.
首先根据等边三角形的性质,得到BC=AC,CD=CE∵△ABC和△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACD=∠ACD+∠ECD,∠ACD=60°,
∴△BCD≌△ACE(SAS),
∴AE=BD,(①正确)
∠CBD=∠CAE,
∵∠BCA=∠ACG=60°,AC=BC,
∴△BCF≌△ACG(ASA),
∴AG=BF,(②正确)
同理:△DFC≌△EGC(ASA),
∴CF=CG,
∴△CFG是等边三角形,
∴∠CFG=∠FCB=60°,
∴FG∥BE,(③正确)
过C作CM⊥AE于M,CN⊥BD于N,
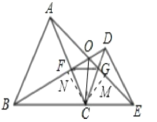
∵△BCD≌△ACE,
∴∠BDC=∠AEC,
∵CD=CE,∠CND=∠CMA=90°,
∴△CDN≌△CEM,
∴CM=CN,
∵CM⊥AE,CN⊥BD,
∴△Rt△OCN≌Rt△OCM(HL)
∴∠BOC=∠EOC,
∴④正确;
故选:D.


科目:初中数学 来源: 题型:
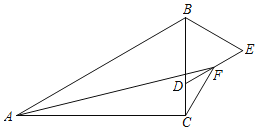
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,点D是BC上一动点,以BD为边在BC的右侧作等边△BDE,F是DE的中点,连结AF,CF,则AF+CF的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() ,其中-3≤a≤1,给出下列结论:①当a=1时,方程组的解也是方程x+y=4-a的解;
,其中-3≤a≤1,给出下列结论:①当a=1时,方程组的解也是方程x+y=4-a的解;
②当a=-2时,x、y的值互为相反数;
③若x<1,则1≤y≤4;
④![]() 是方程组的解,其中正确的结论有
是方程组的解,其中正确的结论有
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】濠河成功晋升国家![]() 级旅游景区,为了保护这条美丽的护城河,南通市政府投入大量资金治理濠河污染,在城郊建立了一个大型污水处理厂,设库池中有待处理的污水
级旅游景区,为了保护这条美丽的护城河,南通市政府投入大量资金治理濠河污染,在城郊建立了一个大型污水处理厂,设库池中有待处理的污水![]() 吨,又从城区流入库池的污水按每小时
吨,又从城区流入库池的污水按每小时![]() 吨的固定流量增加,如果同时开动
吨的固定流量增加,如果同时开动![]() 台机组需
台机组需![]() 小时刚好处理完污水,同时开动
小时刚好处理完污水,同时开动![]() 台机组需
台机组需![]() 小时刚好处理完污水,若需要
小时刚好处理完污水,若需要![]() 小时内将污水处理完毕,那么至少要同时开动多少台机组?(每台机组每小时处理污水量不变)
小时内将污水处理完毕,那么至少要同时开动多少台机组?(每台机组每小时处理污水量不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明学习了《有理数》后,对运算非常感兴趣,于是定义了一种新运算“△”规则如下:对于两个有理数m , n , m △ n =![]() .
.
(1)计算:1△(-2)= ;
(2)判断这种新运算是否具有交换律,并说明理由;
(3)若a![]() =| x-1| , a
=| x-1| , a![]() =| x-2|,求a
=| x-2|,求a![]() △ a
△ a ![]() (用含 x 的式子表示)
(用含 x 的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵![]() 两次共花费940元
两次共花费940元![]() 两次购进的A、B两种花草价格均分别相同
两次购进的A、B两种花草价格均分别相同![]() .
.
![]() 、B两种花草每棵的价格分别是多少元?
、B两种花草每棵的价格分别是多少元?
![]() 若再次购买A、B两种花草共12棵
若再次购买A、B两种花草共12棵![]() 、B两种花草价格不变
、B两种花草价格不变![]() ,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.
,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCO的两边OA、OC在坐标轴的正半轴上,![]() 轴,
轴,![]() ,以直线
,以直线![]() 为对称轴的抛物线过A,B,C三点.
为对称轴的抛物线过A,B,C三点.
![]() 求该抛物线的函数解析式;
求该抛物线的函数解析式;
![]() 已知抛物线交x轴的负半轴于点D,直线BD交y轴于点N,点
已知抛物线交x轴的负半轴于点D,直线BD交y轴于点N,点![]() 是线段AD上一个动点,过点E作x轴的垂线交直线BD于点P,交抛物线于点F,求当
是线段AD上一个动点,过点E作x轴的垂线交直线BD于点P,交抛物线于点F,求当![]() 时相应的m的值.
时相应的m的值.
![]() 在
在![]() 的条件下,连接CP以CP为一边向外作正方形CPGH,如图2所示,当正方形的顶点G或顶点H随着点E的运动落在抛物线上时,直接写出此时点E的坐标.
的条件下,连接CP以CP为一边向外作正方形CPGH,如图2所示,当正方形的顶点G或顶点H随着点E的运动落在抛物线上时,直接写出此时点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.

(1)当∠BDA=115°时,∠BAD= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
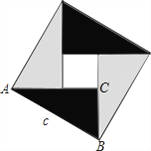
【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若![]() ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:
(1)试说明![]() ;
;
(2)如果大正方形的面积是10,小正方形的面积是2,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com