
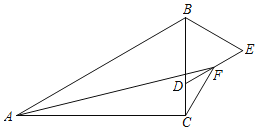
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,点D是BC上一动点,以BD为边在BC的右侧作等边△BDE,F是DE的中点,连结AF,CF,则AF+CF的最小值是_____.
【答案】2![]() .
.
【解析】
以BC为边作等边三角形BCG,连接FG,AG,作GH⊥AC交AC的延长线于H,根据等边三角形的性质得到DC=EG,根据全等三角形的性质得到FC=FG,于是得到在点D的运动过程中,AF+FC=AF+FG,而AF+FG≥AG,当F点移动到AG上时,即A,F,G三点共线时,AF+FC的最小值=AG,根据勾股定理即可得到结论.
以BC为边作等边三角形BCG,连接FG,AG,
作GH⊥AC交AC的延长线于H,
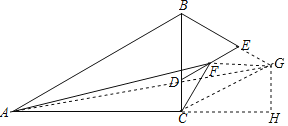
∵△BDE和△BCG是等边三角形,
∴DC=EG,
∴∠FDC=∠FEG=120°,
∵DF=EF,
∴△DFC≌△EFG(SAS),
∴FC=FG,
∴在点D的运动过程中,AF+FC=AF+FG,而AF+FG≥AG,
∴当F点移动到AG上时,即A,F,G三点共线时,AF+FC的最小值=AG,
∵BC=CG=![]() AB=2,AC=2
AB=2,AC=2![]() ,
,
在Rt△CGH中,∠GCH=30°,CG=2,
∴GH=1,CH=![]() ,
,
∴AG=![]() =
=![]() =2
=2![]() ,
,
∴AF+CF的最小值是2![]() .
.


科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第一年的可变成本为2.6万元,设可变成本平均每年增长的百分率为![]()
(1)用含x的代数式表示低3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年的增长百分率x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出A1、B1、C1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2),
其中结论正确的个数是

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AM∥CN,求证:
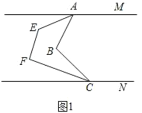

①∠MAB+∠ABC+∠BCN=360°;
②∠MAE+∠AEF+∠EFC+∠FCN=540°;
(2)如图2,若平行线AM与CN间有n个点,根据(1)中的结论写出你的猜想并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() ,若平移点
,若平移点![]() 到点
到点![]() ,使以点
,使以点![]() 为顶点的四边形是菱形,则正确的平移方法是( )
为顶点的四边形是菱形,则正确的平移方法是( )

A. 向左平移(![]() )个单位,再向上平移1个单位
)个单位,再向上平移1个单位
B. 向左平移![]() 个单位,再向下平移1个单位
个单位,再向下平移1个单位
C. 向右平移![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
D. 向右平移2个单位,再向上平移1个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长沙市马王堆蔬菜批发市场某批发商原计划以每千克10元的单价对外批发销售某种蔬菜![]() 为了加快销售,该批发商对价格进行两次下调后,售价降为每千克
为了加快销售,该批发商对价格进行两次下调后,售价降为每千克![]() 元.
元.
![]() 求平均每次下调的百分率;
求平均每次下调的百分率;
![]() 某大型超市准备到该批发商处购买2吨该蔬菜,因数量较多,该批发商决定再给予两种优惠方案以供选择
某大型超市准备到该批发商处购买2吨该蔬菜,因数量较多,该批发商决定再给予两种优惠方案以供选择![]() 方案一:打八折销售;方案二:不打折,每吨优惠现金1000元
方案一:打八折销售;方案二:不打折,每吨优惠现金1000元![]() 试问超市采购员选择哪种方案更优惠?请说明理由.
试问超市采购员选择哪种方案更优惠?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC和△DCE均是等边三角形,点B. C. E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论中:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC,正确的是( )个

A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com