
【题目】如图,四边形ABCD中,已知∠B、∠C的角平分线相交于点O,∠A+∠D =200°,求∠BOC的度数.

【答案】100°
【解析】
已知四边形的内角和为360°,∠A+∠D =200°,可得∠ABC+∠BCD的度数,又因为∠B、∠C的角平分线是OB和OC,根据角平分线性质可得∠OBC+∠OCB的度数,再利用三角形内角和可求出∠BOC的度数.
四边形ABCD中,∠A+∠ABC+∠BCD+∠D=360°
∵∠A+∠D=200°
∴∠ABC+∠BCD=360°-200°=160°
∵BO、CO分别是∠ABC、∠BCD的平分线
∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠BCD
∠BCD
∴∠OBC=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() ×160°=80°
×160°=80°
∵∠BOC+∠OBC+∠OCB=180°
∴∠BOC=180°-80°=100°
∴∠BOC的度数为100°.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】黑板上写有1,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 共100个数字,每次操作先从黑板上的数中选取2个数a,b,然后删去a,b,并在黑板上写上数a+b+1,则经过_____次操作后,黑板上只剩下一个数,这个数是_____.
共100个数字,每次操作先从黑板上的数中选取2个数a,b,然后删去a,b,并在黑板上写上数a+b+1,则经过_____次操作后,黑板上只剩下一个数,这个数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结论:
①若a b c 0 ,且abc 0 ,则方程a bx c 0 的解是 x 1
②若a x 1 bx 1 有唯一的解,则a b;
③若b 2a ,则关于 x 的方程ax b 0a 0的解为 x ![]() ;
;
④若a b c 1,且a 0 ,则 x 1一定是方程ax b c 1的解.其中结论正确个数有( ).
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3![]() 、7
、7![]() 、9
、9![]() ;乙盒子中装有4张卡片,卡片上分别写着2
;乙盒子中装有4张卡片,卡片上分别写着2![]() 、4
、4![]() 、6
、6![]() 、8
、8![]() ;盒子外有一张写着5
;盒子外有一张写着5![]() 的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)定义:直角三角形两直角边的平方和等于斜边的平方。如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=___.

(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP=![]() AD,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为多少?
AD,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A. B两种园艺造型共50个,摆放在迎宾大道两侧。已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆。
(1)某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
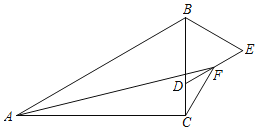
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,点D是BC上一动点,以BD为边在BC的右侧作等边△BDE,F是DE的中点,连结AF,CF,则AF+CF的最小值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com