
���� ��һ��ȡ���������Ϊ���ŵ�������ʣ�µ����������ܱ�2�������ڶ��ΰ�ʣ�µ�����ԭ����λ�ñ�1-100�ţ�ȡ���±�ĵ��ţ���ʣ�µĵ�����ԭ���ı���ܱ�4���������˷���������ȡ�����ʣ�µ�����ԭ���ı���ܱ�8������������ȥ�Ϳ����װ�н�Ʒ���������ţ�
��� �⣺��һ��ȡ�����ǵ��ŵ�����ʣ�µ�����������2�ı�������Ϊԭ����200ֻ�����Ի�ʣ100ֻ��
�ڶ���ȡ����ʣ�µ�����������4�ı��������Ի�ʣ50ֻ��
������ȡ����ʣ�µ�����������8�ı��������Ի�ʣ25ֻ��
���Ĵ�ȡ����ʣ�µ�����������16�ı��������Ի�ʣ12ֻ��
�����ȡ����ʣ�µ�����������32�ı��������Ի�ʣ6ֻ��
������ȡ����ʣ�µ�����������64�ı��������Ի�ʣ3ֻ��
���ߴ�ȡ����ʣ�µ�����������128�ı��������Ի�ʣ1ֻ��
��װ�н�Ʒ����������������128��
�ʴ�Ϊ��128��
���� ���⿼�����ֵı仯���ɣ��������⣬����ÿ��ȡ��������Ǻ�ʣ�µ��������ţ�����֪��װ�н�Ʒ�������������ţ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
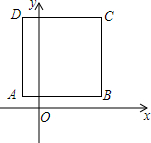 ��ͼ��������ABCD�ı߳�Ϊ4����A������Ϊ��-1��1����ABƽ����x�ᣬ���C������Ϊ��������
��ͼ��������ABCD�ı߳�Ϊ4����A������Ϊ��-1��1����ABƽ����x�ᣬ���C������Ϊ��������| A�� | ��3��1�� | B�� | ��-1��1�� | C�� | ��3��5�� | D�� | ��-1��5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
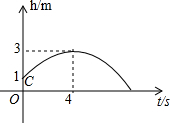 ��ͼ��Ǧ��ij��ֵ�C�����1�ף����ֺ���˶�·���������ߣ����ֺ�4���Ӵﵽ���߶�3�ף���Ǧ������·�ߵĽ���ʽΪh=-$\frac{1}{8}$��t-4��2+3��h=-$\frac{1}{8}$t2+t+1��
��ͼ��Ǧ��ij��ֵ�C�����1�ף����ֺ���˶�·���������ߣ����ֺ�4���Ӵﵽ���߶�3�ף���Ǧ������·�ߵĽ���ʽΪh=-$\frac{1}{8}$��t-4��2+3��h=-$\frac{1}{8}$t2+t+1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����2�� | B�� | 2�� | C�� | 1�� | D�� | 0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com