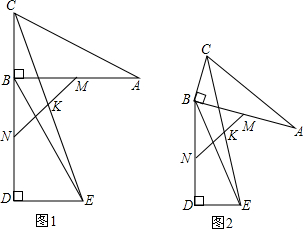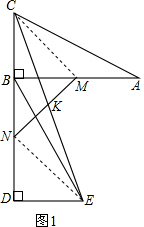
解:(1)CK=EK;
证明:∵BC=DE,AC=BE,∠ABC=∠BDE=90°,
∴△ABC≌△BDE,
∴AB=BD;
∵M、N分别为AB、BD中点,AB=2BC,
∴BM=AM=BC=

AB=

BD=DN=BN,
∴∠BMN=∠BNM=∠DNE=∠BMC=45°,
∴∠CMN=∠MNE=90°,
连接CM、EN,
则△BCM≌△DEN,
∴CM=NE,又∠CKM=∠EKN,
∴△CMK≌△ENK,
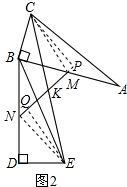
∴CK=EK;
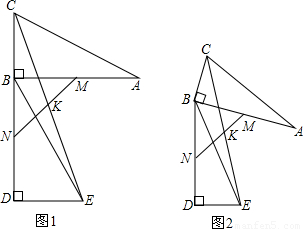
(2)CK=EK;
过C、E分别作直线MK的垂线段,垂足分别为P、Q,
由(1)知△ABC≌△BDE,△BCM≌△DEN,
∴BM=BN,CM=NE,∠DNE=∠CMB,
∴∠BNM=∠BMN,
∴180°-∠BNM-∠DNE=180°-∠BMN-∠CMB,
即∠CMP=∠ENQ,
又∵∠CPM=∠NQE=90°,CM=EN,
∴△CMP≌△ENQ,
∴PC=QE,
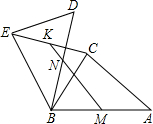
∵∠CPQ=∠EQP=90°,∠EKQ=∠CKP,
∴△CPK≌△EQK,
∴CK=KE;
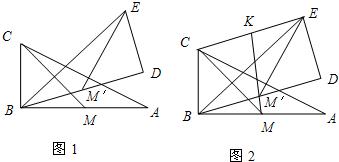
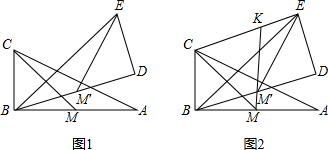
(3)如图,△ABC≌△BDE,M、N分别为AB、DB中点,直线MN交CE于K.
结论:CK=EK.
分析:(1)连接CM、BN,由已知易证得△ABC≌△BDE,可得到AB=BD;再通过证明△BCM≌△DEN,得CN=NE;接下来易证得△CMK≌△ENK,即可得CK=EK.
(2)过C、E分别作直线MK的垂线段,垂足分别为P、Q,首先证明△CMP≌△ENQ,可得PC=QE,然后易证明△CPQ≌△EQK,即得CK=EK.
(3)据题意,画出图形即可.
点评:三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.解答此题的关键在于正确作出辅助线.

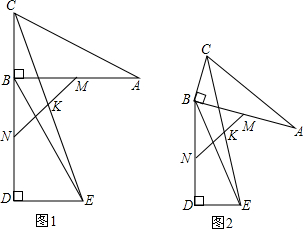
 解:(1)CK=EK;
解:(1)CK=EK; AB=
AB= BD=DN=BN,
BD=DN=BN,