
 如图所示,?ABCD中,∠ADC和∠BCD的平分线交于点M,且分别交AB于E、F.
如图所示,?ABCD中,∠ADC和∠BCD的平分线交于点M,且分别交AB于E、F.分析 (1)由在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,易证得△ADM与△BCN是等腰三角形,继而证得结论;
(2)当四边形ABCD为矩形时,易求得△MFE是等腰直角三角形,然后由勾股定理求得EF=$\sqrt{2}$MF.
解答 (1)AF=BE
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC,
∴∠CDM=∠AMD,∠DCN=∠BNC,
∵∠BCD和∠ADC的平分线分别交AB于M,N两点,
∴∠ADM=∠CDM,∠BCN=∠DCN,
∴∠ADM=∠AMD,∠BCN=∠BNC,
∴AD=AM,BC=BN,
∴AM=BN,
∴AF=BE;
(2)添加∠A=90°.
证明:∵∠A=90°,
∴四边形ABCD为矩形,
∵∠BCD和∠ADC的平分线分别交AB于E,F两点,
∴∠CDM=$\frac{1}{2}$∠ADC=45°,∠DCM=$\frac{1}{2}$∠BCD=45°,
∴∠CDM=∠DCM,∠CDM+∠DCM=$\frac{1}{2}$(∠ADC+∠BCD)=90°,
∴∠DMC=90°=∠FME,
∵AB∥CD,
∴∠CDM=∠MEF,∠DCM=∠MFE,
∴∠MEF=∠MFE,
∴MF=ME,
∴MF2+ME2=EF2,
∴EF=$\sqrt{2}$MF.
点评 此题考查了平行四边形的性质,等腰三角形的判定与性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.


科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 3 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为了测量黄河某一段河流宽度,在河北选了一点A,在河南岸相距200m的B、C两点,分别测得∠ABC=60°,∠ACB=45°,求这段河流的宽度.
如图,为了测量黄河某一段河流宽度,在河北选了一点A,在河南岸相距200m的B、C两点,分别测得∠ABC=60°,∠ACB=45°,求这段河流的宽度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
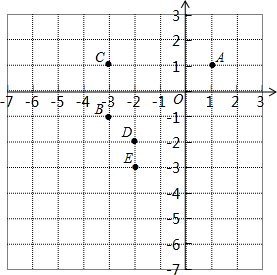 在同一平面直角坐标系中有6个点:
在同一平面直角坐标系中有6个点:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y2+y-6=0 | B. | y2-y-6=0 | C. | y2-y+6=0 | D. | y2-y-6=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | B. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | C. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | D. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com