
【题目】如图,已知线段AB=12cm,点E在AB上,且AE= ![]() AB,延长线段AB到点C,使BC=
AB,延长线段AB到点C,使BC= ![]() AB,点D是BC的中点,求线段DE的长.
AB,点D是BC的中点,求线段DE的长.![]()
科目:初中数学 来源: 题型:
【题目】把代数式mx2-6mx+9m分解因式,下列结果中正确的是( )
A.m(x+3)2
B.m(x+3)(x-3)
C.m(x-4)2
D.m(x-3)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各因式分解正确的是( )
A. x2+2x-1=(x-1)2
B. -x2+(-2)2=(x-2)(x+2)
C. x3-4x = x(x+2)(x-2)
D. (x+1)2= x2+2x+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图l所示,给定线段MN及其垂直平分线上一点P。若以点P为圆心,PM为半径的优弧(或半圆弧)MN上存在三个点可以作为一个等边三角形的顶点,则称点P为线段MN的“三足点”,特别的,若这样的等边三角形只存在一个,则称点P为线段MN的“强三足点”。
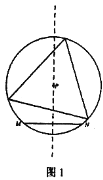
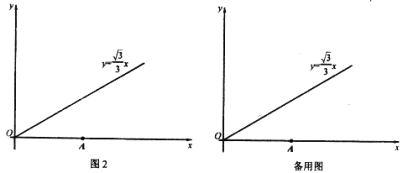
问题:如图2所示,平面直角坐标系xOy中,点A的坐标为(2![]() ,0),点B在射线y=
,0),点B在射线y=![]() x(x≥0)上。
x(x≥0)上。
(1)在点C(![]() ,0),D(
,0),D(![]() ,1),E(
,1),E(![]() ,-2)中,可以成为线段OA的“三足点”的是__________.
,-2)中,可以成为线段OA的“三足点”的是__________.
(2)若第一象限内存在一点Q既是线段OA的“三足点”,又是线段OB的“强三足点”,求点B的坐标。
(3)在(2)的条件下,以点A为圆心,AB为半径作圆,假设该圆与x轴交点中右侧一个为H,圆上一动点K从H出发,绕A顺时针旋转180°后停止,设点K出发后转过的角度为![]() (0°<
(0°< ![]() ≤180°),若线段OB与AK不存在公共“三足点”,请直接写出
≤180°),若线段OB与AK不存在公共“三足点”,请直接写出![]() 的取值范围是_______________。
的取值范围是_______________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解中,正确的是( )
A.﹣2x3﹣3xy3+xy=﹣xy(2x2﹣3y2+1)
B.﹣y2﹣x2=﹣(y+x)(y﹣x)
C.16x2+4y2﹣16xy=4(2x﹣y)2
D.x2y+2xy+4y=y(x+2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC和△DEF的面积分别为S1、S2 .
(1)如图①,AC=DF,BC=DE,∠C=30°,∠D=150°,比较S1与S2的大小为; 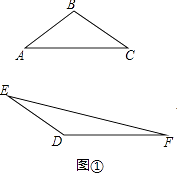
A.S1>S2
B.S1<S2
C.S1=S2
D.不能确定
(2)说明(1)的理由.
(3)如图②,在△ABC与△DEF中,AC=DF,BC=DE,∠C=30°,点E在以D为圆心,DE长为半径的半圆上运动,∠EDF的度数为α,比较S1与S2的大小(直接写出结果,不用说明理由). 
查看答案和解析>>
科目:初中数学 来源: 题型:
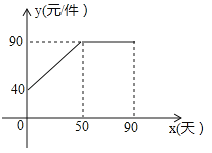
【题目】九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).

(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
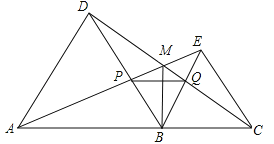
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com