
【题目】如图,已知:AB∥CD,求证:∠B+∠D+∠BED=360°.(至少用三种方法) 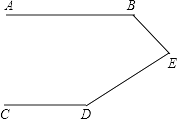
【答案】证明:①连接BD,如图, 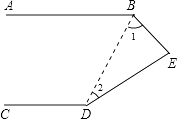
∵AB∥CD(已知),
∴∠ABD+∠CDB=180°(两直线平行,同旁内角互补).
∵∠1+∠2+∠BED=180°(三角形内角和为180°),
∴∠ABD+∠1+∠CDB+∠2+∠BED=360°,
即∠ABE+∠CDE+∠BED=360°.
②延长DE交AB延长线于F,如图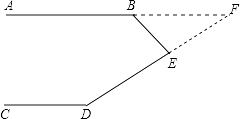
∵AB∥CD(已知),
∴∠F+∠D=180°(两直线平行,同旁内角互补).
∵∠ABE=∠FEB+∠F,
∠BED=∠FBE+∠F(三角形一个外角等于和它不相邻的两个内角的和)
∴∠ABE+∠CDE+∠BED
=∠FEB+∠F+∠CDE+∠FBE+∠F
=180°+180°
=360°.
③过点E作EF∥AB,如图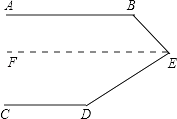
∵AB∥CD,
∴AB∥EF∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠B+∠BEF=180°
∠D+∠DEF=180°(两直线平行,同旁内角互补)
∴∠B+∠BEF+∠D+∠DEF
=180°+180°
=360°.
【解析】要证明∠B+∠D+∠BED=360°,可利用两直线平行,同旁内角互补及三角形内角和定理和三角形外角的性质,作出恰当的辅助线求解.
【考点精析】本题主要考查了平行线的判定与性质和三角形的内角和外角的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】对于多项式:①x2-y2;②-x2-y2;③4x2-y;④x2-4,能够用平方差公式进行因式分解的是( )
A. ①和② B. ①和③ C. ①和④ D. ②和④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB中,A、B两点的坐标分别为(2,5),(6,2),把△AOB向下平移3个单位,向左平移2个单位,得到△CDE.
(1)写出C、D、E三点的坐标,并在图中画出△CDE.
(2)求出△CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若函数y=ax2﹣2x+a的图象与坐标轴只有1个交点,则a的取值范围是( )
A.a≥1B.a>1或a=0
C.a≥1或a=0D.a>1或a=0或a<﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为4,且△ABC是直角三角形,则满足条件的点C有( )个.
A. 7 B. 8 C. 5 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com