Question

【题目】如图，已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，求证：AB=AC+BD．

Answer 1

【答案】证明：在AB上取一点F，使AF=AC，连结EF．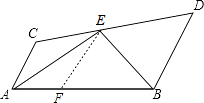
∵EA、EB分别平分∠CAB和∠DBA，
∴∠CAE=∠FAE，∠EBF=∠EBD．
∵AC∥BD，
∴∠C+∠D=180°．
在△ACE和△AFE中，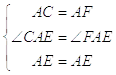
，
∴△ACE≌△AFE（SAS），
∴∠C=∠AFE．
∵∠AFE+∠EFB=180°，
∴∠EFB=∠D．
在△BEF和△BED中，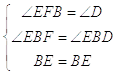
，
∴△BEF≌△BED（AAS），
∴BF=BD．
∵AB=AF+BF，
∴AB=AC+BD．
【解析】在AB上取一点F，使AF=AC，连结EF，就可以得出△ACE≌△AFE，就有∠C=∠AFE．由平行线的性质就有∠C+∠D=180°，由∠AFE+∠EFB=180°得出∠EFB=∠D，在证明△BEF≌△BED就可以得出BF=BD，进而就可以得出结论．