
【题目】(1)如图![]() 示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.

(2)现在如图b示,仍有AB∥CD,但点E在AB与CD的上方,①请尝试探索∠1,∠2,∠E三者的数量关系. ②请说明理由.
【答案】(1)证明见解析(2)∠1+∠2-∠E=180°
【解析】
试题(1)过点E作EF∥AB,由两直线平行,内错角相等,得到∠A=∠1.
由平行的传递性得到EF // CD,再由平行线的性质得到∠2=∠C,由角的和差即可得到结论;
(2)过点E作EF∥AB,类似可得到结论.
试题解析:解:(1)过点E作EF∥AB,∴∠A=∠1(两直线平行,内错角相等).
∵AB // CD(已知),∴EF // CD(平行的传递性),∴∠2=∠C(两直线平行,内错角相等).
∵∠AEC=∠1+∠2(图上可知),∴∠AEC=∠A+∠C(等量代换) ;
(2)∠1+∠2-∠E=180°.理由如下:
过点E作EF∥AB,∴∠4+∠1=180°(两直线平行,同旁内角互补).
∵AB // CD(已知),∴EF // CD(平行的传递性),∴∠FEC=∠2(两直线平行,内错角相等),即∠3+∠4=∠2,∴∠4=∠2-∠3(等式性质),∴∠2-∠3+∠1=180°(等量代换),
即∠1+∠2-∠AEC=180°.



科目:初中数学 来源: 题型:
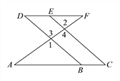
【题目】如图,E点为DF上的点,B为AC上的点,![]() ,
,![]() ,求证:DF∥AC.
,求证:DF∥AC.
证明:∵ ![]() (已知),∠1=∠3,∠2=∠4( ),
(已知),∠1=∠3,∠2=∠4( ),
∴∠3=∠4(等量代换).
∴__________![]() __________( ).
__________( ).
∴∠C=∠ABD( ).
∵∠C=∠D( ),
∴∠D=__________( ).
∴AC∥DF( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,某市政府的一项实事工程就是由政府投入1 000万元资金,对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造,某社区为配合政府完成该项工作,对社区内1 200户家庭中的120户进行了随机抽样调查,并汇总成下表:
改造情况 | 均不改造 | ||||||
改造水龙头 | 改造马桶 | ||||||
1个 | 2个 | 3个 | 4个 | 1个 | 2个 | ||
户数 | 20 | 31 | 28 | 21 | 12 | 69 | 2 |
(1)试估计该社区需要对水龙头或马桶进行改造的家庭共有___户;
(2)改造后,一个水龙头一年大概可节约5吨水,一个马桶一年大约可节约15吨水,试估计该社区一年共可节约多少吨水?
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如图两幅统计图(不完整).
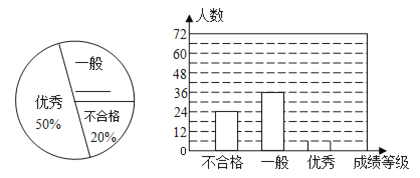
请你根据图中所给的信息解答下列问题:
(1)这次测试,一共抽取了名学生;
(2)请将以上两幅统计图补充完整;(注:扇形图补百分比,条形图补“优秀”人数与高度);
(3)若“一般”和“优秀”均被视为达标成绩,该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且∠AOB=60°,反比例函数![]() (k>0)在第一象限内过点A,且与BC交于点F.(1)若OA=10,求反比例函数的解析式;
(k>0)在第一象限内过点A,且与BC交于点F.(1)若OA=10,求反比例函数的解析式;
(2)若F为BC的中点,且S△AOF=24![]() ,求OA长及点C坐标;
,求OA长及点C坐标;
(3)在(2)的条件下,过点F作EF∥OB交OA于点E(如图2),若点P是直线EF上一个动点,连结,PA,PO,问是否存在点P,使得以P,A,O三点构成的三角形是直角三角形?若存在,请指出这样的P点有几个,并直接写出其中二个P点坐标;若不存在,请说明了理由.
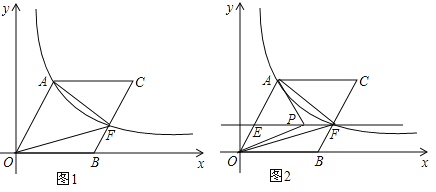
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠C=90°,AB的垂直平分线MN交BC于点D.
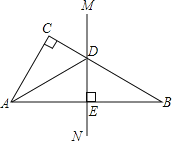
(1)如果∠CAD=20°,求∠B的度数;
(2)如果∠CAB=50°,求∠CAD的度数;
(3)如果∠CAD:∠DAB=1:2,求∠CAB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用长度相等的小棒按一定规律摆成的一组图案.
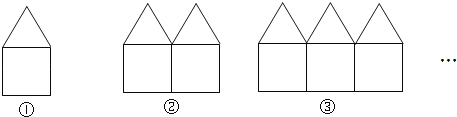
(1)第1个图案中有______根小棒;第2个图案中有__根小棒;第3个图案中有__根小棒;
(2)第n个图案中有多少根小棒?
(3)第25个图案中有多少根小棒?
(4)是否存在某个符合上述规律的图案,由2032根小棒摆成?如果有,指出是第几个图案;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(8,6),∠CAO的平分线与y轴相交于点D,则点D的坐标为_____.
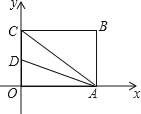
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com