

 ∠COD=22.5°,
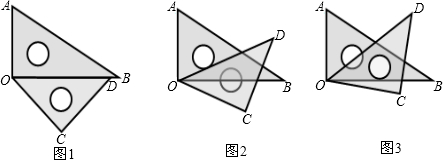
∠COD=22.5°, ∠COD=22.5°,则∠AOC=∠AOB+∠COB=112.5°,于是可得到∠AOC+∠BOD=112.5°+22.5°=135°;
∠COD=22.5°,则∠AOC=∠AOB+∠COB=112.5°,于是可得到∠AOC+∠BOD=112.5°+22.5°=135°;

 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
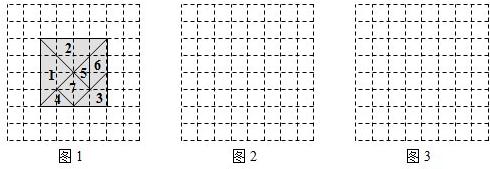
 25、七巧板是我们祖先创造的一种智力玩具,如图,整副七巧板是由一个正方形分割成七小块而成(其中:五块等腰直角三角形、一块正方形和一块平行四边形),用这七小块可以拼出各种各样的漂亮图案.请用这七小块拼出一个等腰梯形,并在网格中画出图形.
25、七巧板是我们祖先创造的一种智力玩具,如图,整副七巧板是由一个正方形分割成七小块而成(其中:五块等腰直角三角形、一块正方形和一块平行四边形),用这七小块可以拼出各种各样的漂亮图案.请用这七小块拼出一个等腰梯形,并在网格中画出图形.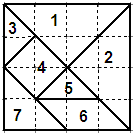
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com