
【题目】解方程组、不等式组:
(1)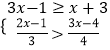
(2)![]() .
.
【答案】
(1)解: 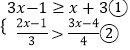
∵解不等式①得:x≥2,
解不等式②得:x<8,
∴不等式组的解集为:2≤x<8
(2)解:整理得: ![]()
①﹣②×3得:﹣10x=12.5,
解得:x=﹣1.25,
把x=﹣1.25代入②得:﹣7.5﹣3y=2.5,
y=﹣ ![]() ,
,
所以原方程组的解为: 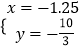
【解析】(1)先求出不等式的解集,再求出不等式组的解集即可;(2)①﹣②×3得出﹣10x=12.5,求出x,把x=﹣1.25代入②求出y即可.
【考点精析】通过灵活运用解二元一次方程组和一元一次不等式组的解法,掌握二元一次方程组:①代入消元法;②加减消元法;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )即可以解答此题.


科目:初中数学 来源: 题型:
【题目】某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道,其余部分铺上草皮.
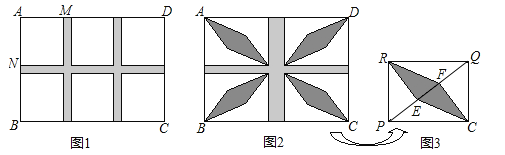
(1)如图1,若设计三条通道,一条横向,两条纵向,且它们的宽度相等,其余六块草坪相同,其中一块草坪两边之比AM:AN=8:9,问通道的宽是多少?
(2)为了建造花坛,要修改(1)中的方案,如图2,将三条通道改为两条通道,纵向的宽度改为横向宽度的2倍,其余四块草坪相同,且每一块草坪均有一边长为8m,这样能在这些草坪建造花坛.如图3,在草坪RPCQ中,已知RE⊥PQ于点E,CF⊥PQ于点F,求花坛RECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车制造厂开发一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 两条直线的位置关系只有相交和平行两种
B. 在同一平面内,不相交的两条线段互相平行
C. 在同一平面内,不相交的两条直线互相平行
D. 在同一平面内,不相交的两条射线互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙,丙,丁四名跳高运动员赛前几次选拔赛成绩如表所示,根据表中的信息,如果要从中,选择一名成绩好又发挥稳定的运动员参加比赛,那么应选_____.
甲 | 乙 | 丙 | 丁 | |
平均数(cm) | 185 | 180 | 185 | 180 |
方差 | 3.6 | 3.6 | 7.9 | 8.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com