
【题目】如图,在平面直角坐标系中,A(![]() ,1),B(2
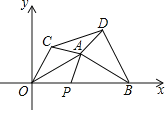
,1),B(2![]() ,0),点P为线段OB上一动点,将△AOP沿AO翻折得到△AOC,将△ABP沿AB翻折得到△ABD,则△ACD面积的最小值为_____.
,0),点P为线段OB上一动点,将△AOP沿AO翻折得到△AOC,将△ABP沿AB翻折得到△ABD,则△ACD面积的最小值为_____.
【答案】![]()
【解析】
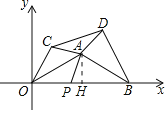
如详解图,作AH⊥OB于H.首先证明∠OAB=120°,再证明△CAD是顶角为120°的等腰三角形,最后根据垂线段最短解决问题即可.
解:如图,作AH⊥OB于H.
∵A(![]() ,1),
,1),
∴OH=![]() ,AH=1,
,AH=1,
∴tan∠OAH=![]() =
=![]() ,
,
∴∠OAH=60°,
∵B(2![]() ,0),
,0),
∴OH=HB=![]() ,
,
∵AH⊥OB,
∴AO=AB,
∴∠OAH=∠BAH=60°,
由翻折的性质可知:AP=AC=AD,∠PAO=∠CAO,∠BAP=∠BAD,
∴∠OAC+∠BAD=∠OAB=120°,
∴∠CAD=360°﹣2×120°=120°,
∴△CAD是顶角为120°的等腰三角形,
根据垂线段最短可知,当AP与AH重合时,AC=AD=PA=1,
此时△ACD的面积最小,最小值=![]() ×1×1sin60°=
×1×1sin60°=![]() .
.
故答案为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图题:(不写画法)
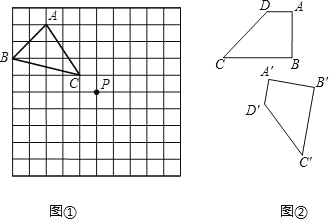
(1)如图①,在 10×10 的正方形网格中,每个小正方形的边长为1个单位. 请作出△ABC 绕点P逆时针旋转 90°的△A′B′C′;
(2)如图②,四边形A′B′C′D′是由四边形ABCD绕某一点旋转得到的,请通过作图确定这个点,并把它命名为点O,再把四边形ABCD关于点O的中心对称图形A′B′C′D′画出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,∠BAC=90°,D为AC边上一动点,且不与点A点C重合,连接BD并延长,在BD延长线上取一点E,使AE=AB,连接CE.
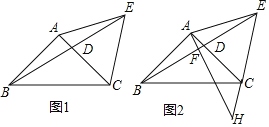
(1)若∠AED=20°,则∠DEC= 度;
(2)若∠AED=a,试探索∠AED与∠AEC有怎样的数量关系?并证明你的猜想;
(3)如图2,过点A作AF⊥BE于点F,AF的延长线与EC的延长线交于点H,求证:EH2+CH2=2AE2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节放假期间,小明和小华准备到宜宾的蜀南竹海(记为A)、兴文石海(记为B)、夕佳山居民(记为C)、李庄古镇(记为D)中的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点被选中的可能性相同.
(1)小明选择去蜀南竹海旅游的概率为________;
(2)用画树状图或列表的方法求小明和小华都选择去兴文石海旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个数的平方等于![]() ,记为
,记为![]() ,这个数
,这个数![]() 叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为![]() (
(![]() 为实数),
为实数),![]() 叫这个复数的实部,
叫这个复数的实部, ![]() 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
例如计算: ![]()
(1)填空: ![]() =_________,
=_________, ![]() =____________.
=____________.
(2)填空:①![]() _________; ②
_________; ②![]() _________ 。
_________ 。
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知, ![]() ,(
,( ![]() 为实数),求
为实数),求![]() 的值。
的值。
(4)试一试:请利用以前学习的有关知识将![]() 化简成
化简成![]() 的形式。
的形式。
(5)解方程:x2 - 2x +4 = 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:直线y=ax+b与直线y=bx+a互为“友好直线”.如:直线y=2x+1与直线y=x+2互为“友好直线”.
(1)点M(m,2)在直线y=-x+4的“友好直线”上,则m=________;
(2)直线y=4x+3上的一点M(m,n)又是它的“友好直线”上的点,求点M的坐标;
(3)对于直线y=ax+b上的任意一点M(m,n),都有点N(2m,m-2n)在它的“友好直线”上,求直线y=ax+b的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com