
 三个顶点的坐标分别为
三个顶点的坐标分别为

 ,并求出
,并求出 所在直线的解析式。
所在直线的解析式。 绕点
绕点 顺时针旋转
顺时针旋转 后得到的
后得到的 ,并求出
,并求出 在上述旋转过程中扫过的面积。
在上述旋转过程中扫过的面积。 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
 矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上
矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上
 ,OA=1,OC=2,
,OA=1,OC=2, 点D在边OC上且
点D在边OC上且 .
. y轴上
y轴上 是否存在点P,直线PD与矩形对角线AC交于点M,使得
是否存在点P,直线PD与矩形对角线AC交于点M,使得 为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由. 抛物线
抛物线 经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且
经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且 沿DE折叠后点O落在边AB上
沿DE折叠后点O落在边AB上 处?
处?
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
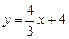 分别交
分别交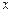 轴,
轴,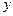 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.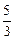 个单位长度的速度向终点B运动,过点P作
个单位长度的速度向终点B运动,过点P作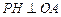 ,垂足为H,连接
,垂足为H,连接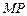 ,
,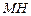 .设点P的运动时间为
.设点P的运动时间为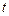 秒.
秒. 的值;
的值; 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.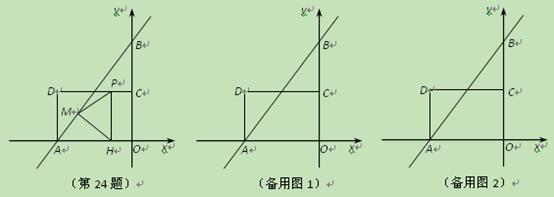
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com