
【题目】如图,已知EC∥AB,∠EDA=∠ABF. 
(1)求证:四边形ABCD是平行四边形;
(2)求证:OA2=OEOF.
 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2∥l3 , 等腰Rt△ABC的三个顶点A,B,C分别在l1 , l2 , l3上,∠ ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则AB:BD的值为( ) 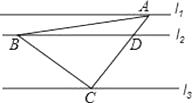
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D,E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH= ![]() ,CH=5
,CH=5 ![]() .
. 
(1)求证:AH是⊙O的切线;
(2)若点D是弧CE的中点,且AD交CE于点F,求证:HF=HA;
(3)在(2)的条件下,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家园林公司承接了哈尔滨市平房区园林绿化工程,已知乙公司单独完成所需要的天数是甲公司单独完成所需天数的1.5倍,如果甲公司单独工作10天,再由乙公司单独工作15天,这样就可完成整个工程的三分之二.
(1)求甲、乙两公司单独完成这项工程各需多少天?
(2)上级要求该工程完成的时间不得超过30天.甲、乙两公司合作若干天后,甲公司另有项目离开,剩下的工程由乙公司单独完成,并且在规定时间内完成,求甲、乙两公司合作至少多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A、B两种园艺造型共50个,摆放在迎宾大道两侧.已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆.
(1)某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP. 
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com