
(1)、菱形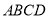 的边长1,面积为
的边长1,面积为 ,则
,则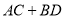 的值为( )
的值为( )
A、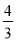 B、
B、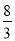 C、
C、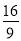 D、
D、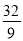
(2)、如图,ABCD是正方形,E是CF上一点,若DBEF是菱形,则∠EBC=

(1)B;(2)15°.
【解析】
试题分析:(1)在菱形ABCD中,设AO=x,BO=y,根据菱形的性质得出: 求出x、y的值即可求出AC+BD的值.
求出x、y的值即可求出AC+BD的值.
(2)过D作DG垂直于CF,垂足为G,由正方形的性质可得出正方形的四条边相等,且四个角为直角,三角形BCD为等腰直角三角形,可得出∠BDC与∠DBC都为45°,设正方形的边长为1,根据勾股定理求出BD的长为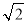 ,即菱形的四条边为
,即菱形的四条边为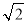 ,由DG与FC垂直,且BD与EF平行,可得BD垂直于DG,进而得到∠CDG为45°,即三角形DCG为等腰直角三角形,由DC的长为1,可求出DG为
,由DG与FC垂直,且BD与EF平行,可得BD垂直于DG,进而得到∠CDG为45°,即三角形DCG为等腰直角三角形,由DC的长为1,可求出DG为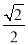 ,在直角三角形DFG中,由DG为DF的一半,得到∠F为30°,再根据菱形的对角相等,可得∠DBE为30°,由∠EBC=∠DBC∠DBE求出度数即可.
,在直角三角形DFG中,由DG为DF的一半,得到∠F为30°,再根据菱形的对角相等,可得∠DBE为30°,由∠EBC=∠DBC∠DBE求出度数即可.
(1)在菱形ABCD中,设AO=x,BO=y,
根据菱形的性质得出: 解得
解得
∴AC+BD=2(x+y)=2×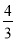 =
=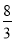 .
.
故选B.
(2)过D作DG⊥CF,垂足为G,如图所示:
∵四边形ABCD为正方形,
∴∠CBD=∠CDB=45°,∠BCD=90°,
设正方形ABCD的边长为1,即AB=BC=CD=AD=1,
∴根据勾股定理得:BD=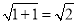 ,
,
∵四边形BEFD为菱形,
∴BE=EF=DF=BD=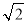 ,
,
又BD∥EF,DG⊥FC,
∴BD⊥DG,即∠BDG=90°,
∴∠CDG=∠BDG∠BDC=90°45°=45°,又∠DGC=90°,
∴△DCG为等腰直角三角形,又DC=1,
∴DG=DCsin45°=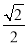 ,
,
又DF=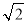 ,
,
在Rt△DFG中,由DG=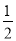 DF,
DF,
∴∠F=30°,
∴∠DBE=30°,
则∠EBC=∠DBC∠DBE=45°30°=15°.
考点:1.正方形的性质;2.菱形的性质.


科目:初中数学 来源:2015届浙江省温州市六校八年级下学期期中联考数学试卷(解析版) 题型:解答题
为了了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:

根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生800人,女生760人,请估计身高在 之间的学生约有多少人?
之间的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源:2015届浙江省八年级下学期期中考试数学试卷(解析版) 题型:选择题
下列说法不正确的是( )
A.有两组对边分别平行的四边形是平行四边形
B.平行四边形的对角线互相平分
C.平行四边形的对角互补,邻角相等
D.平行四边形的对边平行且相等
查看答案和解析>>
科目:初中数学 来源:2015届浙江省嘉兴市八年级下学期期中检测数学试卷(解析版) 题型:选择题
不能判定四边形ABCD为平行四边形的题设是( )
A.AB=CD AB ∥CD B.∠A=∠C ∠B=∠D
C.AB=AD BC=CD D.AB=CD AD=BC
查看答案和解析>>
科目:初中数学 来源:2015届浙江省台州市八年级下学期期中考试数学试卷(解析版) 题型:解答题
如图,直线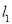 ,
,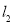 相交于点
相交于点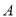 ,
,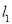 与
与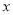 轴的交点坐标为
轴的交点坐标为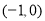 ,
,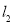 与
与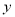 轴的交点坐标为
轴的交点坐标为 ,结合图象解答下列问题:(每小题4分,共8分)
,结合图象解答下列问题:(每小题4分,共8分)
(1)求直线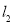 表示的一次函数的表达式;
表示的一次函数的表达式;
(2)当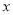 为何值时,
为何值时,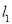 ,
,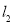 表示的两个一次函数值都大于
表示的两个一次函数值都大于 .
.

查看答案和解析>>
科目:初中数学 来源:2015届河南省郑州市八年级下学期期末考试数学试卷(解析版) 题型:解答题
小明、小华、小刚三人在一起讨论一个一元一次不等式组.
小明:其中一个不等式的解集为x≤8;
小刚:其中有一个不等式在求解的过程中需要改变不等号方向;
请你写出符合上述条件的不等式组,并解这个不等式组.
查看答案和解析>>
科目:初中数学 来源:2015届河南平顶山华英学校八年级下学级第一次月考数学试卷(解析版) 题型:解答题
有一群猴子,一天结伴去偷桃子.分桃子时,如果每只猴子分3个,那么还剩下59个;如果每个猴子分5个,就都分得桃子,但有一个猴子分得的桃子不够5个.你能求出有几只猴子,几个桃子吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com