精英家教网 > 初中数学 > 题目详情

（1） $数学公式$
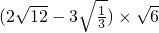
（2）tan²60°+4sin30°cos45°-（π-5）⁰．

（1）解：原式=2 $\text{[math]}$ -3 $\text{[math]}$
=12 $\text{[math]}$ -3 $\text{[math]}$
=9 $\text{[math]}$ ；

（2）解：原式=（ $\text{[math]}$ ）²+4× $\text{[math]}$ × $\text{[math]}$ -1
=3+ $\text{[math]}$ -1
=2+ $\text{[math]}$ ．
故答案为：9 $\text{[math]}$ ，2+ $\text{[math]}$ ．
分析：（1）根据二次根式混合运算的法则把括号内的每一项分别同 $\text{[math]}$ 相乘，再把所得结果化为最简二次根式的形式，再合并同类项；
（2）分别根据特殊角的三角函数值及0指数幂的运算法则计算出各数，再根据实数混合运算的法则进行计算．
点评：本题考查的是二次根式的混合运算，特殊角的三角函数值及0指数幂的运算法则，熟知以上知识是解答此题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

某校组织学生到涪江河某段测量两岸的距离，采用了两种方案收集数据．
方案一：如图，从C点找准对岸一参照点D，使CD垂直于河岸线l，沿河岸行走至E点，测出CE的长度后，再用电子测角器测出CE与ED的夹角α；
方案二：如图，先从河岸上选一点A，测出A到河面的距离h．再用电子测角器测出A点到对岸河面的俯角β．

（1）学生们选用不同的位置测量后得出以下数据，请通过计算填写下表：（精确到0.1米）
方案一：

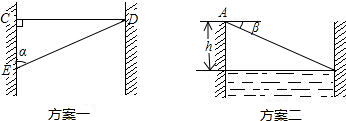
测量次数	1	2	3
EC（单位：米）	100	150	200
α	76°33′	71°35′	65°25′
计算得出河宽（单位：米）

方案二：

测量次数	1	2	3
EC（单位：米）	14.4	13.8	12.5
β	1°24′	2°16′	1°56′
计算得出河宽（单位：米）

（参考数据：tan1°24′=0.0244、tan2°16′=0.0396、tan1°56′=0.0338、tan76°33′=4.1814、tan71°35′=3.0032、tan65°25′=2.1859）
（2）由（1）表中数据计算：
方案一中河两岸平均宽为

米；
方案二中河两岸平均宽为

米；
（3）判断河两岸宽大约为

米；（从下面三个答案中选取，填入序号）
①390～420 ②420～450 ③350～480
（4）求出方案一的方差S₁²和方案二的方差S₂²，判断用哪种方案测量的误差较小．（精确到1）

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，矩形ABCD中，AB=8，BC=10，点P在矩形的边DC上由D向C运动．沿直线AP翻折△ADP，形成如下四种情形．设DP=x，△ADP和矩形重叠部分（阴影）的面积为y．

（1）如图丁，当点P运动到与C重合时，求重叠部分的面积y；
（2）如图乙，当点P运动到何处时，翻折△ADP后，点D恰好落在BC边上这时重叠部分的面积y等于多少？
（3）阅读材料：已知锐角α≠45°，tan2α是角2α的正切值，它可以用角α的正切值tanα来表示，即tan2α=

2tanα

1-(tanα)2

（α≠45°）．根据上述阅读材料，求出用x表示y的解析式，并指出x的取值范围．
（提示：在图丙中可设∠DAP=a）

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，AB为⊙O直径，CD为弦，AD与BC交于点E，∠CEA=α，则

S△CDE

S△ABE

的值等于（　　）

A、cosα

B、sin²α

C、cos²α

D、tan²α

查看答案和解析>>

科目：初中数学 来源： 题型：

已知：sinα是关于x的一元二次方程2x²+3x-2=0的一个根，请计算代数式：tan²α-sinα+2cosα的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

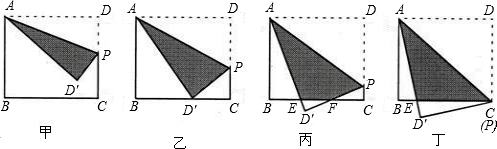
如图，挂着“庆祝海门实验学校建校三周年”条幅的氢气球升在校园上空，已知气球的直径为4m，在地面A点测得气球中心O的仰角为∠OAD=60°，测得气球的视角∠BAC=2°（AB、AC为⊙O的切线，B、C为切点）．则气球中心O离地面的高度OD约为多少？
（精确到1m，参考数据：sin1°=0.0175，sin2°=0.0349，tan1°=0.0175，tan2°=0.0350，

=1.732）

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学

（1）（2）tan260°+4sin30°cos45°-（π-5）0．

（1） $数学公式$
（2）tan²60°+4sin30°cos45°-（π-5）⁰．