Question

【题目】如图，在平面直角坐标系中，一次函数y=ax+b的图象与反比例函数y=的图象交于一、三象限内的A、B两点，与x轴交于C点，点A的坐标为（2，m），点B的坐标为（n，﹣2），tan∠BOC= ．
（1）求该反比例函数和一次函数的解析式．
（2）求△BOC的面积．
（3）P是x轴上的点，且△PAC的面积与△BOC的面积相等，求P点的坐标．

Answer 1

【答案】解：（1）过B作x轴的垂线，垂足为D，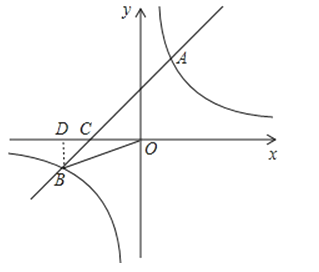

∵B的坐标为（n，﹣2），
∴BD=2，
∵tan∠BOC=，
∴OD=4，
∴B的坐标为（﹣4，﹣2）
把B（﹣4，﹣2）代入y=得：k=8，
∴反比例函数为y=，
把A（2，m）代入y=得：m=4，
∴A（2，4），
把A（2，4）和B（﹣4，﹣2）代入y=ax+b得：
解得：a=1，b=2，
∴一次函数的解析式为：y=x+2；
（2）在y=x+2中，令y=0，得x=﹣2，
∴CO=2，
∴S△BOC=COBD=×2×2=2；
（3）设P点的坐标为P（a，0）
则由S△PAC=S△BOC得：PC×4=2，
∴PC=1，
即||a+2|=1，
解得：a=﹣3或a=﹣1，
即P的坐标为（﹣3，0）或（﹣1，0）．
【解析】（1）过B作x轴的垂线，垂足为D，求出BD=2，根据tan∠BOC=求出OD=4，得出B的坐标，把B的坐标代入y=即可求出反比例函数的解析式，求出A的坐标，把A、B的坐标代入一次函数的解析式，即可求出解析式；
（2）求出CO=2，根据三角形面积公式求出即可；
（3）设P点的坐标为P（a，0）根据S△PAC=S△BOC得出PC×4=2，求出PC即可．