
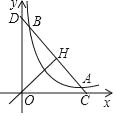
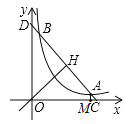
【题目】如图,已知直线y=﹣x+b(b>0)与其垂线y=x交于H,与双曲线c:y=![]() (k>0)在第一象限交于A,B,与两坐标轴交于C,D.
(k>0)在第一象限交于A,B,与两坐标轴交于C,D.
(1)当A的坐标为(2,1)时,求k的值和OH的长;
(2)若CH2﹣HA2=4,求双曲线c的方程.
【答案】(1)OH=![]() ;(2)设双曲线c的方程为y=
;(2)设双曲线c的方程为y=![]() .
.
【解析】分析:(1)将A(2,1)代入y=![]() ,可得k=2,过A作AM⊥x轴于M,则AM=MC=1,OM=2,可得OC=OM+MC=3,依据∠HOC=45°,即可得到OH=
,可得k=2,过A作AM⊥x轴于M,则AM=MC=1,OM=2,可得OC=OM+MC=3,依据∠HOC=45°,即可得到OH=![]() OC=
OC=![]() ;
;
(2)设点A的坐标为(x,y)且x>y,则OC=OM+MC=x+y,OH=HC=![]() OC=
OC=![]() (x+y),进而得出HA=HC﹣AC=
(x+y),进而得出HA=HC﹣AC=![]() (x﹣y),根据CH2﹣HA2=[
(x﹣y),根据CH2﹣HA2=[![]() (x+y)]2﹣[
(x+y)]2﹣[![]() (x﹣y)]2=2xy=2k=4,即可得到k的值.
(x﹣y)]2=2xy=2k=4,即可得到k的值.
详解:(1)将A(2,1)代入y=![]() ,可得:k=2×1=2,
,可得:k=2×1=2,
过A作AM⊥x轴于M,则AM=MC=1,OM=2,∴OC=OM+MC=3.
∵∠HOC=45°,∴OH=![]() OC=
OC=![]() ;
;
(2)设点A的坐标为(x,y)且x>y,则OC=OM+MC=x+y,OH=HC=![]() OC=
OC=![]() (x+y).
(x+y).
又∵AC=![]() AM=
AM=![]() y,∴HA=HC﹣AC=
y,∴HA=HC﹣AC=![]() (x﹣y).
(x﹣y).
∵CH2﹣HA2=[![]() (x+y)]2﹣[
(x+y)]2﹣[![]() (x﹣y)]2=2xy=2k=4,∴k=2,
(x﹣y)]2=2xy=2k=4,∴k=2,
∴双曲线c的方程为y=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
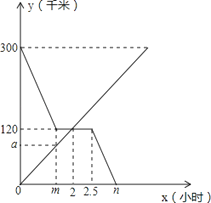
(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
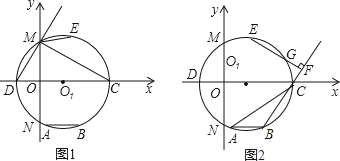
【题目】已知,如图:O1为x轴上一点,以O1为圆心作⊙O1交x轴于C、D两点,交y轴于M、N两点,∠CMD的外角平分线交⊙O1于点E,AB是弦,且AB∥CD,直线DM的解析式为y=3x+3.
(1)如图1,求⊙O1半径及点E的坐标.
(2)如图2,过E作EF⊥BC于F,若A、B为弧CND上两动点且弦AB∥CD,试问:BF+CF与AC之间是否存在某种等量关系?请写出你的结论,并证明.
(3)在(2)的条件下,EF交⊙O1于点G,问弦BG的长度是否变化?若不变直接写出BG的长(不写过程),若变化自画图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线1上有A,B两点,AB=12cm,点O是线段AB上的一点,OA=2OB.
(1)OA=______cm,OB=______cm;
(2)若点C是线段AB上一点(点C不与点AB重合),且满足AC=CO+CB,求CO的长;
(3)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s.设运动时间为t(s),当点P与点Q重合时,P,Q两点停止运动.求当t为何值时,2OP-OQ=4(cm);
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网店店主小李进了一批某种商品,每件进价10元.预售一段时间后发现:每天销售量![]() (件)与售价
(件)与售价![]() (元/件)之间成一次函数关系:
(元/件)之间成一次函数关系:![]() .
.
(1)小李想每天赚取利润150元,又要使所进的货尽快脱手,则售价定为多少合适?
(2)小李想每天赚取利润300元,这个想法能实现吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知点![]() 及直线
及直线![]() ,根据下列要求画图:
,根据下列要求画图:

(1)作直线![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ;
;
(2)画线段![]() ,并取
,并取![]() 的中点
的中点![]() ,作射线
,作射线![]() ;
;
(3)连接![]() 并延长至点
并延长至点![]() ,使得
,使得![]()
(4)请在直线![]() 上确定一点
上确定一点![]() ,使点
,使点![]() 到点
到点![]() 与点
与点![]() 的距离之和
的距离之和![]() 最小.
最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:等腰△ABC中,AB=AC,点D在AC右侧,∠BAC=∠BDC=120°
(1)猜想DA,DC,DB的数量关系并证明
(2)点D 在AB边左侧时三条线段关系是否发生变化?请画出图形。若变化,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日,是第23个世界读书日.为了推进中华传统文化教育,营造浓厚的读书氛围,我市某学校举办了“让读书成为习惯,让书香溢病校园”主题活动.为了解学生每周阅读时间,该校随机抽取了部分学生进行调查,根据调查结果,将阅诙时间![]() (单位:小时)分成了
(单位:小时)分成了![]() 组,
组, ![]()
![]()
![]() ,下图是根据这组数据绘制的两幅不完整的统计图.请你结合图中所给信息解答下列问题:
,下图是根据这组数据绘制的两幅不完整的统计图.请你结合图中所给信息解答下列问题:
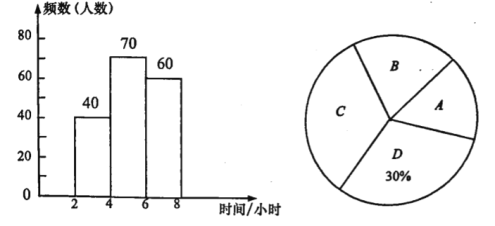
(1)这次随机抽取了 名学生进行调查;
(2)补全频数分布直方图;
(3)计算扇形统计图中扇形![]() 的圆心角的度数;
的圆心角的度数;
(4)若该校共有![]() 名学生,请你估计每周阅读时间不足
名学生,请你估计每周阅读时间不足![]() 小时的学生共有多少名?
小时的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD.
(1)求证:BD=BF;
(2)若AB=10,CD=4,求BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com