练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
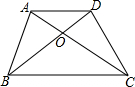
    8．加图，在四边形ABCD中，AD∥BC，AD=1，BC=3，那么S△AOD：S四边形ABCD的值为多少？

    分析 由梯形ABCD中AD∥BC，可得△AOD∽△COB，然后由相似三角形面积比等于相似比的平方，求得△BOC的面积，又由等高三角形的面积的比等于对应底的比，可求得△AOB与△COD的面积，继而求得答案．

    解答 解：∵梯形ABCD中AD∥BC，
    ∴△AOD∽△COB，
    ∴OA：OC=AD：BC=1：3，
    ∴S△AOD：S△BOC=1：9，
    设S△AOD=x，
    ∴S△BOC=9S△AOD=9x，
    ∴S△AOB=S△COD=3S△AOD=3x，
    ∴梯形ABCD的面积为：S△AOD+S△AOB+S△BOC+S△COD=15x．
    ∴S△AOD：S四边形ABCD的值=x：15x=1：15．

    点评 此题考查了梯形的性质以及相似三角形的判定与性，熟练掌握相似三角形的判定和性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．在△ABC中，∠ACB=90°，AB的垂直平分线交AB于D，交AC于E，交BC延长线于F，DF=6，DE=4，求CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．在Rt△ABC中，∠C=90°，BC=AC，AB=8，点D在AB边上，点E是BC边上一点（不与点B、C重合），且DA=DE，则AD的取值范围是8$\sqrt{2}$-8≤AD＜4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．在△ABC中，BC=a，AC=b，AB=c；
    （1）若∠C为直角，则a2+b2=c2；
    （2）若∠C为锐角，则a2+b2与c2的关系为a2+b2-c2＞0；请解答：若∠C为钝角，试推到a2+b2与c2的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，在四边形ABCD中，∠A=30°，∠B=60°，AB=8，BC=2，AD=3$\sqrt{3}$．求四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，在△ABC中，∠BAC=90°，AD⊥BC，∠BAD=30°，AE为BC边上的中线，求证：AE=AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

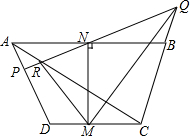    20．等腰梯形ABCD中，M和N分别为CD、AB的中点．过N作直线PQ和AD和CB的延长线分别交于P和Q，AC和PQ交于点R，求证：∠NMR=∠NMQ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．用代数式表示：
    （1）x的3倍与3的差：3x-3．
    （2）x的2与y的$\frac{1}{2}$的和：2x+$\frac{1}{2}$y．
    （3）a与b的和的平方：（a+b）2．
    （4）2与a的立方的商：$\frac{2}{{a}^{3}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．在6张完全相同的卡片是分别画上角、等边三角形，不含直角且邻边不相等的平行四边形、直角梯形、正方形和圆，在看不见图形的情况下随机摸出1张，这张卡片上的图形是轴对称图形的概率是$\frac{2}{3}$．

    查看答案和解析>>

    同步练习册答案