
【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
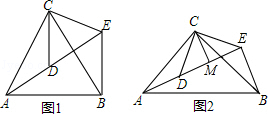
【答案】(1)60°;(2)∠AEB=90°AE= BE+2CM.
【解析】解:(1)∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=60°﹣∠DCB =∠BCE.
在△ACD和△BCE中,
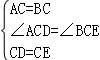 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°,
∴∠BEC=120°.
∴∠AEB=∠BEC﹣∠CED=60°.
(2)
∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°
∴CA=CB,CD=CE.
且∠ACD=∠BCE.
在△ACD和△BCE中,
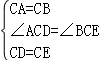 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°,
∴∠BEC=135°.
∴∠AEB=∠BEC﹣∠CED=90°.
∵CD=CE,CM⊥DE,
∴DM=ME.
∵∠DCE=90°,
∴DM=ME=CM.
∴AE=AD+DE=BE+2CM.


科目:初中数学 来源: 题型:
【题目】
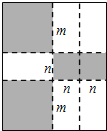
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.
(1)用含m、n的代数式表示切痕的总长为_____________厘米;
(2)若每块小矩形的面积为48厘米2,四个正方形的面积和为200厘米2,试求(m+n)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
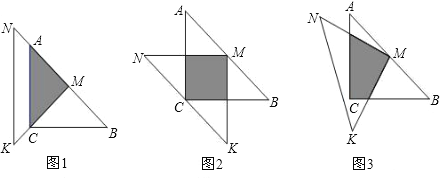
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 ,周长为 .
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 ,周长为 .
2(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (2016湖南湘西州第14题)一个等腰三角形一边长为4cm,另一边长为5cm,那么这个等腰三角形的周长是( )
A.13cm B.14cm C.13cm或14cm D.以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学竞赛初试有试题25道,阅卷规定:每答对一题得4分,每答错(包括未答)一题得(﹣1)分,得分不低于60分则可以参加复试.那么,若要参加复试,初试的答对题数至少为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a、b的值是( )
A.a=5,b=1 B.a=-5,b=1
C.a=5,b=-1 D.a=-5,b=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学知识竞赛共有30道题,规定,答对一道题得4分,不答或答错一道题倒扣2分,若甲同学答对25题,答错5道题,则甲 同学得________分,若得分低于60分者获奖,则获奖者至少应答对________道题。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点M在第四象限,到x轴,y轴的距离分别为6,4,则点M的坐标为( )
A. (4,﹣6) B. (﹣4,6) C. (﹣6,4) D. (﹣6,﹣4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com