
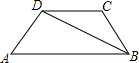
 如图,在等腰梯形ABCD中,AB∥CD,AD=BC=4,∠A=60°,BD平分∠ABC,则这个梯形的面积是( )
如图,在等腰梯形ABCD中,AB∥CD,AD=BC=4,∠A=60°,BD平分∠ABC,则这个梯形的面积是( )A、6
| ||
B、8
| ||
C、10
| ||
D、12
|
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
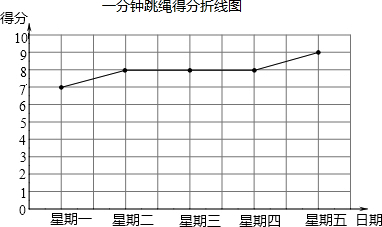 我市体育中考规定:可以在立定跳远和1分钟跳绳中任选一项测试,同学们将根据自己平时的运动成绩确定自己的报考项目,下面是小亮同学在近期的两个项目中连续五次测试的得分情况(立定跳远得分统计表和1分钟跳绳得分折线图).
我市体育中考规定:可以在立定跳远和1分钟跳绳中任选一项测试,同学们将根据自己平时的运动成绩确定自己的报考项目,下面是小亮同学在近期的两个项目中连续五次测试的得分情况(立定跳远得分统计表和1分钟跳绳得分折线图).| 测试日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 得分 | 7 | 10 | 8 | 9 | 6 |
| 统计量 | 平均数 | 极差 | 方差 |
| 立定跳远得分 | 8 | ||
| 1分钟跳绳得分 | 2 | 0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
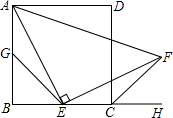 如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com