Question

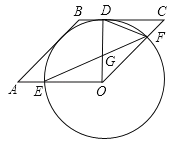
【题目】已知：四边形OABC是菱形，以O为圆心作⊙O，与BC相切于点D，交OA于E，交OC于F，连接OD，DF．

（1）求证：AB是⊙O的切线；

（2）连接EF交OD于点G，若∠C=45°，求证：GF2=DGOE．

Answer 1

【答案】（1）证明见解析；（2）证明见解析．

【解析】试题分析：（1）过O作OH⊥AB，由菱形的性质可求得OH=OD，由切线的性质可知OD为圆O的半径，可得OH为圆O的半径，可证得结论；

（2）由条件可证明△DGF∽△DFO，再利用相似三角形的性质可证得结论．

试题解析：解：

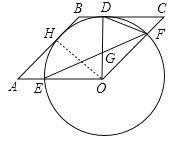
（1）如图，过O作OH⊥AB，∵四边形OABC为菱形，∴AB=BC，∵BC为⊙O的切线，∴OD⊥BC，且OD为⊙O的半径，∴ABOH=BCOD，∴OH=OD，∴AB为⊙O的切线；

（2）由（1）可知OD⊥CB，∴AO⊥DO，∴∠AOD=90°，∴∠DFO=∠AOD=45°，∵∠C=45°，且∠ODC=90°，∴∠DOF=45°，在△OGF中，∠DGF为△OGF的外角，∴∠DGF=∠DOF+∠GFO=45°+∠GFO，∵∠DFO=∠DFG+∠GFO=45°+∠GFO，∴∠DGF=∠DFO，且∠GDF=∠FDO，∴△DGF∽△DFO，∴，即DFGF=DGOF，∵OF=OD=OE，∴DF=GF，∴GF2=DGOE．