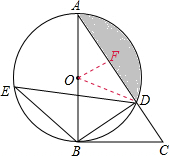
解:(1)证明:∵AB为⊙O的直径,∴∠ADB=90°,即∠ABD+∠BAD=90°.
又∵∠CBD=∠E,∠BAD=∠E,∴∠ABD+∠CBD=90°,即∠ADC=90°.
∴BC⊥AB.∴BC是⊙O的切线.
(2)当点E运动到DE经过点O位置时,△EDB≌△ABD.证明如下:
当点E运动到DE经过点O位置时,∠EBD=∠ADB=90°,
在△EDB与△ABD中,
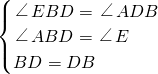
,
∴△EDB≌△ABD(AAS).
(3)如图,连接OD,过点O作OF⊥AD于点F,
∵∠BAD=∠E,tanE=

,
∴tan∠BAD=

.
又∵∠ADB=90°,
∴∠BAD=30°.
∵∠ABC=90°,BC=

,
∴AB=
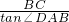
=4.
∴AO=2,OF=1,AF=AOcos∠BAD=

.
∴AD=2

.
∵AO=DO,
∴∠AOD=120°.
∴S
阴影=S
扇形OAD-S
△AOD=

-

×3=2

×1=

π-

≈2.5.
分析:(1)欲证明BC是⊙O的切线,只需证得BC⊥AB;
(2)利用圆周角定理,全等三角形的判定定理AAS证得当点E运动到DE经过点O位置时,△EDB≌△ABD;
(3)如图,连接OD,过点O作OF⊥AD于点F.S
阴影=S
扇形OAD-S
△AOD.由圆周角定理和正切三角函数定义易求AB的长度、圆心角∠AOD=120°.所以根据扇形面积公式和三角形的面积公式进行计算即可.
点评:本题考查了切线的判定、全等三角形的判定以及扇形面积的计算.求(3)题中阴影部分的面积时,采用了“分割法”.

 如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED.
如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED. ,BC=
,BC= ,求阴影部分的面积.(计算结果精确到0.1)
,求阴影部分的面积.(计算结果精确到0.1) ≈1.41,
≈1.41, ≈1.73)
≈1.73) 解:(1)证明:∵AB为⊙O的直径,∴∠ADB=90°,即∠ABD+∠BAD=90°.
解:(1)证明:∵AB为⊙O的直径,∴∠ADB=90°,即∠ABD+∠BAD=90°.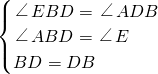 ,
, ,
, .
. ,
,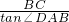 =4.
=4. .
. .
. -
- ×3=2
×3=2 ×1=
×1= π-
π- ≈2.5.
≈2.5.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为