解:(1)∵PD∥AB,
∴
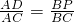
.
∵BC=4,AC=

,BP的长为x,
∴
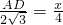
.
∴

;
(2)过点P作PE⊥AC于E.
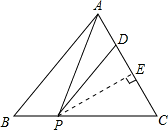
∵sin∠ACB=
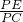
,∠C=60°,
∴PE=PC×sin60°=

(4-x).
∴y=

AD•PE=

•

x•

(4-x)=-

x
2+

x.
∴y与x之间的函数关系式为:y=-

x
2+

x.
∴当x=2时,y的值最大,最大值是

;
(3)点P存在这样的位置.
∵△ADP与△ABP等高不等底,
∴
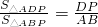
.
∵△ADP的面积是△ABP面积的

,
∴
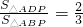
.
∴
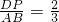
.
∵PD∥AB,
∴△CDP∽△CAB.
∴
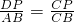
.
∴

.
∴
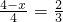
.
∴
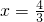
.
∴
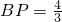
.
答:(1)AD的长为

x;
(2)y与x之间的函数关系式是y=-

x
2+

x,当x等于2时,y的值最大,最大值是

;
(3)存在这样的位置,BP的长是

.
分析:(1)根据PD∥AB,利用平行线分线段成比例,可得
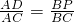
,然后将已知数值代入即可.
(2)过点P作PE⊥AC于E.利用sin∠ACB=
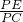
,∠C=60°,求得PE,然后即可求出y与x之间的函数关系式.
(3)根据△ADP与△ABP等高不等底,可得
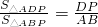
.根据△ADP的面积是△ABP面积的

,可得
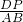
=

.再利用PD∥AB,可得△CDP∽△CAB.然后利用相似三角形对应边成比例即可求得BP.从而可得点P存在这样的位置.
点评:此题主要考查相似三角形的判定与性质,二次函数的最值,平行线分线段成比例等知识点,综合性强,有一定的拔高难度,是一道典型的题目.

 ,点P在BC边上运动,PD∥AB,交AC于D.
,点P在BC边上运动,PD∥AB,交AC于D.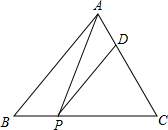 设BP的长为x,△APD的面积为y.
设BP的长为x,△APD的面积为y. ?若存在,请求出BP的长;若不存在,请说明理由.
?若存在,请求出BP的长;若不存在,请说明理由.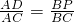 .
. ,BP的长为x,
,BP的长为x,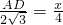 .
. ;
;
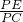 ,∠C=60°,
,∠C=60°, (4-x).
(4-x). AD•PE=
AD•PE= •
• x•
x• (4-x)=-
(4-x)=- x2+
x2+ x.
x. x2+
x2+ x.
x. ;
;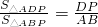 .
. ,
,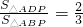 .
.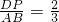 .
.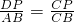 .
. .
.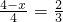 .
.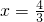 .
.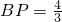 .
. x;
x; x2+
x2+ x,当x等于2时,y的值最大,最大值是
x,当x等于2时,y的值最大,最大值是 ;
; .
.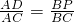 ,然后将已知数值代入即可.
,然后将已知数值代入即可.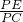 ,∠C=60°,求得PE,然后即可求出y与x之间的函数关系式.
,∠C=60°,求得PE,然后即可求出y与x之间的函数关系式.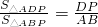 .根据△ADP的面积是△ABP面积的
.根据△ADP的面积是△ABP面积的 ,可得
,可得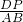 =
= .再利用PD∥AB,可得△CDP∽△CAB.然后利用相似三角形对应边成比例即可求得BP.从而可得点P存在这样的位置.
.再利用PD∥AB,可得△CDP∽△CAB.然后利用相似三角形对应边成比例即可求得BP.从而可得点P存在这样的位置.

 名校课堂系列答案
名校课堂系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为