
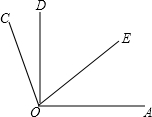
 如图,OE为∠AOD的平分线,∠COD=
如图,OE为∠AOD的平分线,∠COD=| 1 |
| 4 |


科目:初中数学 来源: 题型:
| 伸长长度(cm) | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| 挂物重量(kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
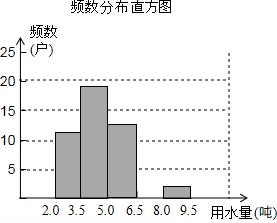 某市在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽取获得的50个家庭去年的月人均用水量(单位:吨)的调查数据进行研究了如下整理:
某市在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽取获得的50个家庭去年的月人均用水量(单位:吨)的调查数据进行研究了如下整理:| 频数分布表 | ||
| 分组 | 频数 | 频率 |
| 2.0<x≤3.5 | 11 | 0.22 |
| 3.5<x≤5.0 | 19 | 0.38 |
| 5.0<x≤6.5 | 13 | 0.26 |
| 6.5<x≤8.0 | ||
| 8.0以上 | 2 | 0.04 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
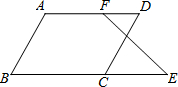 在括号内填写理由.
在括号内填写理由.查看答案和解析>>
科目:初中数学 来源: 题型:
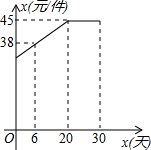 某商人在我县开办了一家儿童服装专卖店,该店在儿童节前5月31日采购进一种今年流行的服装,6月份(6月1日至6月30日)进行30天的试销售,购进价格为20元/件.销售结束后,得知日销售量y(件)与销售时间x(天)之间的函数关系为:
某商人在我县开办了一家儿童服装专卖店,该店在儿童节前5月31日采购进一种今年流行的服装,6月份(6月1日至6月30日)进行30天的试销售,购进价格为20元/件.销售结束后,得知日销售量y(件)与销售时间x(天)之间的函数关系为:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
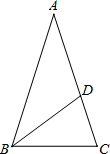 如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com