

 BC,即当1<x≤1.5时,重合部分是个梯形,可用相似三角形求出梯形的上底的长,进而根据梯形的面积计算公式得出S,x的函数关系式.
BC,即当1<x≤1.5时,重合部分是个梯形,可用相似三角形求出梯形的上底的长,进而根据梯形的面积计算公式得出S,x的函数关系式. BC,但D在EG上或EG右侧,即当1.5<x≤2时,此时重合部分是个梯形,如果设EG与AD相交于点M,AD的延长线与FG相交于点N,可先在相似三角形GMN和GEF中求出MN的长,而后根据MD=MN-DN求出梯形的上底长,进而可按梯形的面积计算公式得出S,x的函数关系式.
BC,但D在EG上或EG右侧,即当1.5<x≤2时,此时重合部分是个梯形,如果设EG与AD相交于点M,AD的延长线与FG相交于点N,可先在相似三角形GMN和GEF中求出MN的长,而后根据MD=MN-DN求出梯形的上底长,进而可按梯形的面积计算公式得出S,x的函数关系式. EF•FG=
EF•FG= x2(0<x≤1);
x2(0<x≤1); (MN+EF)FN=x-
(MN+EF)FN=x- (1<x≤1.5);
(1<x≤1.5); (MD+EC)CD=-x+
(MD+EC)CD=-x+ (1.5<x≤2)
(1.5<x≤2) CE•CM=
CE•CM= x2-3x+
x2-3x+ (2<x<3);
(2<x<3);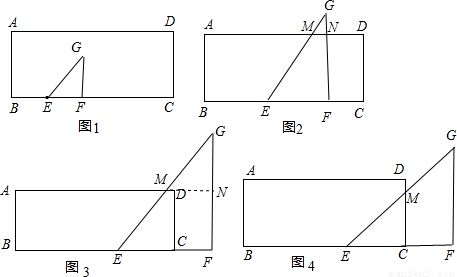


科目:初中数学 来源:2009年辽宁省大连市中考数学二模试卷(解析版) 题型:解答题
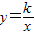 与直线y=ax+b相交于点A(1,5),B(m,-2).
与直线y=ax+b相交于点A(1,5),B(m,-2). 的解集(直接写出答案).
的解集(直接写出答案).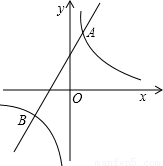
查看答案和解析>>
科目:初中数学 来源:2010年江西省师大附中(南昌市三校)九年级(下)第二次联考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年山东省日照市中考数学模拟试卷4(郑世业)(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2009年辽宁省大连市中考数学二模试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com