
 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )| A. | ($\frac{\sqrt{2}}{2}$)2013 | B. | ($\frac{\sqrt{2}}{2}$)2014 | C. | ($\frac{1}{2}$)2013 | D. | ($\frac{1}{2}$)2014 |
分析 根据等腰直角三角形的性质结合三角形的面积公式可得出部分Sn的值,根据面积的变化即可找出变化规律“Sn=4×$(\frac{1}{2})^{n-1}$”,依此规律即可解决问题.
解答 解:观察,发现:S1=22=4,S2=$(2×\frac{\sqrt{2}}{2})^{2}$=2,S3=$(\sqrt{2}×\frac{\sqrt{2}}{2})^{2}$=1,S4=$(1×\frac{\sqrt{2}}{2})^{2}$=$\frac{1}{2}$,…,
∴Sn=$[2×(\frac{\sqrt{2}}{2})^{n-1}]^{2}$=4×$(\frac{1}{2})^{n-1}$,
∴S2016=4×$(\frac{1}{2})^{2016-1}$=$(\frac{1}{2})^{2013}$.
故选C.
点评 本题考查了等腰直角三角形的性质、三角形的面积、正方形的面积以及规律型中数字的变化类,根据面积的变化找出变化规律“Sn=4×$(\frac{1}{2})^{n-1}$”是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,点P是Rt△ABC斜边AC的中点,动点E、F分别在AB、BC上且保持∠EPF=45°,若以P为圆心的圆与AB相切,试探究动直线EF与⊙P的位置关系,并证明你的结论.
如图,点P是Rt△ABC斜边AC的中点,动点E、F分别在AB、BC上且保持∠EPF=45°,若以P为圆心的圆与AB相切,试探究动直线EF与⊙P的位置关系,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在△ABC中,AB=AC,∠BAC=150°,点A到BC的距离为1,与AB重合的一条射线AP,从AB开始,以每秒15°的速度绕点A逆时针匀速旋转,到达AC后立即以相同的速度返回AB,到达后立即重复上述旋转过程,设AP与BC边的交点为M,旋转2019秒时,BM=2,CM=2+2$\sqrt{3}$.
在△ABC中,AB=AC,∠BAC=150°,点A到BC的距离为1,与AB重合的一条射线AP,从AB开始,以每秒15°的速度绕点A逆时针匀速旋转,到达AC后立即以相同的速度返回AB,到达后立即重复上述旋转过程,设AP与BC边的交点为M,旋转2019秒时,BM=2,CM=2+2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
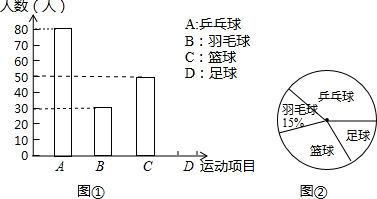
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
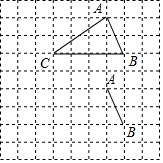 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
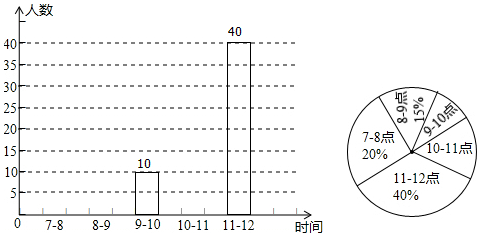
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )
如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )| A. | 4 | B. | $\frac{3}{10}$ | C. | $\frac{10}{3}$ | D. | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com