
 如图,点P是Rt△ABC斜边AC的中点,动点E、F分别在AB、BC上且保持∠EPF=45°,若以P为圆心的圆与AB相切,试探究动直线EF与⊙P的位置关系,并证明你的结论.
如图,点P是Rt△ABC斜边AC的中点,动点E、F分别在AB、BC上且保持∠EPF=45°,若以P为圆心的圆与AB相切,试探究动直线EF与⊙P的位置关系,并证明你的结论. 分析 由题意可证明△PEB∽△FPC,△PEB∽△FPC,则得出点P到AB和EF的距离相等,即可得出结论.
解答 解:直线EF与⊙P相切,理由如下:
在△PEB和△FPC中,∠EPB+∠FPC=135°,∠EPB+∠PEB=135°,
∴∠FPC=∠PEB.
又∵∠B=∠C,
∴△PEB∽△FPC.
∴$\frac{BE}{CP}$=$\frac{EP}{CF}$.
∵△PEB∽△FPC,
∴$\frac{BE}{CP}$=$\frac{PE}{PF}$.
∴$\frac{BE}{BP}$=$\frac{PE}{P}$.
又∵∠B=∠EOF=45°,
∴△BEP∽△PEF.
∴∠BEP=∠PEF.
∴点P到AB和EF的距离相等.
∵AB与⊙O相切,
∴点O到EF的距离等于⊙O的半径.
∴EF与⊙P相切.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质以及切线的性质,是一道综合题,难度偏大.


科目:初中数学 来源: 题型:填空题
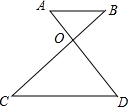 如图,AB∥CD,AD与BC交于点O,若$\frac{OC}{OD}$=$\frac{5}{3}$,则$\frac{AO}{BO}$=$\frac{5}{3}$.
如图,AB∥CD,AD与BC交于点O,若$\frac{OC}{OD}$=$\frac{5}{3}$,则$\frac{AO}{BO}$=$\frac{5}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
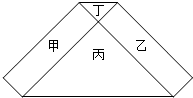 如图的六边形是由甲、乙两个矩形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和,已知丙的直角边长为2,丁的直角边长为a(a<2),求a的值.
如图的六边形是由甲、乙两个矩形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和,已知丙的直角边长为2,丁的直角边长为a(a<2),求a的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )| A. | ($\frac{\sqrt{2}}{2}$)2013 | B. | ($\frac{\sqrt{2}}{2}$)2014 | C. | ($\frac{1}{2}$)2013 | D. | ($\frac{1}{2}$)2014 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com