
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据二次根式有意义的条件对①进行判断;根据平方根的定义对②进行判断;根据判别式的意义和特殊角的三角函数值对③进行判断;根据一元二次方程根的定义对④进行判断;根据反比例函数的性质对⑤进行判断.
解答 解:若式子$\sqrt{x-1}$有意义,则x≥1,所以①错误;
3$\sqrt{2}$是18的平方根,所以②正确;
若关于x的方程x2-$\sqrt{2}$x+cosα=0有两个相等的实数根,则△=2-4cosα=0,cosα=$\frac{1}{2}$,所以锐角α为60°,所以③正确;
x=2是方程x2-6x+c=0的一个实数根,则4-12+c=0,解得c=8,所以④正确;
在反比例函数y=$\frac{k-2}{x}$中,若k>2,在每一象限,y随x的增大而减小,所以⑤错误.
故选C.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.


科目:初中数学 来源: 题型:选择题
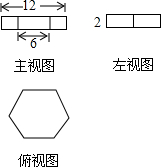 如图所示是某几何体的三视图,则该几何体的体积是( )
如图所示是某几何体的三视图,则该几何体的体积是( )| A. | 18$\sqrt{3}$ | B. | 54$\sqrt{3}$ | C. | 108$\sqrt{3}$ | D. | 216$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
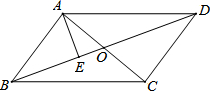 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AE⊥BD于点E.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AE⊥BD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
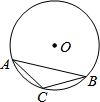 如图,△ABC 内接于⊙O,∠A=30°,⊙O的直径为4cm,则点O到BC的距离是( )
如图,△ABC 内接于⊙O,∠A=30°,⊙O的直径为4cm,则点O到BC的距离是( )| A. | $\sqrt{3}$cm | B. | $\frac{\sqrt{3}}{2}$cm | C. | $\frac{\sqrt{3}}{3}$cm | D. | 2$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{25}{12}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
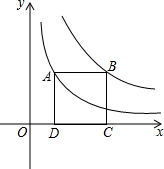 如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{6}{x}$上,且AB∥x轴,C、D在x轴上,若四边形ABCD为正方形,则AB=2.
如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{6}{x}$上,且AB∥x轴,C、D在x轴上,若四边形ABCD为正方形,则AB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com