Question

2．设△ABC的面积为1，如图①，将边BC、AC分别2等分，BE₁、AD₁相交于点O，△AOB的面积记为S₁；如图②将边BC、AC分别3等分，BE₁、AD₁相交于点O，△AOB的面积记为S₂；…，依此类推，则S_n可表示为（　　）（用含n的代数式表示，其中n为正整数）

• A． $\frac{1}{n}$
• B． $\frac{1}{n+1}$
• C． $\frac{1}{2n+1}$
• D． $\frac{1}{2n+2}$

Answer 1

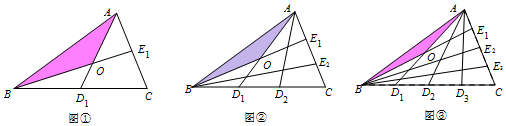
分析 连接D₁E₁，设AD₁、BE₁交于点M，先求出S_△ABE1=$\frac{1}{n+1}$，再根据$\frac{AB}{{D}_{1}{E}_{1}}$=$\frac{BM}{{ME}_{1}}$=$\frac{n+1}{n}$得出S_△ABM：S_△ABE1=n+1：2n+1，最后根据S_△ABM：$\frac{1}{n+1}$=n+1：2n+1，即可求出S_△ABM的值．

解答 解：如图，连接D₁E₁，设AD₁、BE₁交于点M，
∵AE₁：AC=1：n+1，
∴S_△ABE1：S_△ABC=1：n+1，
∴S_△ABE1=$\frac{1}{n+1}$，
∵$\frac{AB}{{D}_{1}{E}_{1}}$=$\frac{BM}{{ME}_{1}}$=$\frac{n+1}{n}$，
∴$\frac{BM}{{BE}_{1}}$=$\frac{n+1}{2n+1}$，
∴S_△ABM：S_△ABE1=n+1：2n+1，
∴S_△ABM：$\frac{1}{n+1}$=n+1：2n+1，
∴S_△ABM=$\frac{1}{2n+1}$．
故选C．

点评 此题考查了相似三角形的判定与性质，用到的知识点是相似三角形的判定与性质、平行线分线段成比例定理、三角形的面积，关键是根据题意作出辅助线，得出相似三角形．