
��ͼ1����������ABCD�У���E��F�ֱ��DZ�BC��AB�ϵĵ㣬��CE=BF.����DE������E��EG��DE��ʹEG=DE.����FG��FC.
��1�����жϣ�FG��CE��������ϵ�� ��λ�ù�ϵ�� ��
��2����ͼ2������E��F�ֱ���CB��BA�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ����������жϲ�����֤����
��3����ͼ3������E��F�ֱ���BC��AB�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ��������ֱ��д������ж�.

 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д� ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}+\sqrt{7}=\sqrt{10}$ | B�� | $\sqrt{{{��-2��}^2}}$=4 | C�� | $\root{3}{27}$=3 | D�� | $\sqrt{\frac{5}{2}}=\frac{{\sqrt{5}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ʵ��a��b�������ϵ�λ����ͼ��ʾ����|a+b|+|a-b|�Ľ���ǣ�������
��ʵ��a��b�������ϵ�λ����ͼ��ʾ����|a+b|+|a-b|�Ľ���ǣ�������| A�� | -2b | B�� | b | C�� | -2a | D�� | 2a-b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�ܿ����е�һ��ģ�⿼����ѧ�Ծ��������棩 ���ͣ��ж���
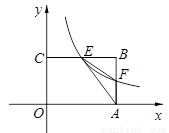
��ͼ���ھ���OABC�У�OA��3��OC��2��F��AB�ϵ�һ�����㣨F��A��B���غϣ�������F�ķ���������y�� ��ͼ�����BC���ڵ�E��
��ͼ�����BC���ڵ�E��
��1����FΪAB���е�ʱ����ú����Ľ���ʽ��
��2����kΪ��ֵʱ����EFA���������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�ܿ����е�һ��ģ�⿼����ѧ�Ծ��������棩 ���ͣ������
����6��7��1����72��1����74��1����78��1����716��1����1��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��㶫ʡ�����о��꼶��ѧ��3���¿���ѧ�Ծ��������棩 ���ͣ��ж���
��ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��EF����O����AB��CD�ֱ��ڵ�E��F����֤����AOE?��COF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�콭��ʡ�����о��꼶��ѧ�ڵ�һ�Σ�3�£��¿���ѧ�Ծ��������棩 ���ͣ���ѡ��
��֪�Ϧ��͡Ϧ»�Ϊ��ǣ����Ϧ�=40�㣬��Ϧµ��ڣ�������
A. 40�� B. 50�� C. 60�� D. 140��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com