
����Ŀ�������������һ���߳�Ϊn��n��2�����������ε�������n�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬 ��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ����أ�
����̽����Ҫ�о���������⣬���Dz����ȴ��������֣������ҵ�һ�����
̽��һ����һ���߳�Ϊ2���������ε�������ƽ�֣����Ӹ����е㣬��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣�
��ͼ1�����ӱ߳�Ϊ2���������������ߵ��е㣬�������£�����1+2+3=6����㣮�߳�Ϊ1���������Σ���һ����1�����ڶ�����2��������1+2=3�����߶���Ϊ3��3=9�����߳�Ϊ2������������1�����߶���Ϊ3�����ܹ���3����1+2+1��=2����1+2+3��=12���߶Σ�

̽��������һ���߳�Ϊ3���������ε����������ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣�
��ͼ2�����ӱ߳�Ϊ3���������������ߵĶ�Ӧ���ȷֵ㣬�������£�����1+2+3+4=10����㣮�߳�Ϊ1���������Σ���һ����1�����ڶ�����2������������3��������1+2+3=6�����߶���Ϊ3��6=18�����߳�Ϊ2������������1+2=3�����߶���Ϊ3��3=9�����߳�Ϊ3������������1�����߶���Ϊ3�����ܹ���3����1+2+3+1+2+1��=3����1+2+3+4��=30���߶Σ�
̽������
�����������ķ�����̽�����߳�Ϊ4���������ε��������ĵȷ֣�ͼ3�������Ӹ��߶�Ӧ�ĵȷֵ㣬�������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣�
������ʾ��ͼ����д��̽�����̣�
��������
�����������ķ�����̽����һ���߳�Ϊn��n��2�����������ε�������n�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣���д��̽�����̣�
ʵ��Ӧ�ã�
��һ���߳�Ϊ30���������ε���������ʮ�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣�
���𰸡�̽������������Ϊ10�����߶���Ϊ60������������������Ϊ![]() �����߶���Ϊ
�����߶���Ϊ![]() ����ʵ��Ӧ�ã�������Ϊ465�����߶���Ϊ14880��
����ʵ��Ӧ�ã�������Ϊ465�����߶���Ϊ14880��
��������
̽����������̽��һ��̽�����ķ�����⼴�ɣ�
������������̽��һ��̽������̽�����Ĺ����ܽ���ɼ��ɣ�
ʵ��Ӧ�ã����ݡ������������ܽ�Ĺ�����⼴�ɣ�
�⣺̽��������ͼ3�У�
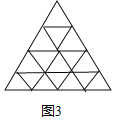
���ӱ߳�Ϊ4���������������ߵĶ�Ӧ�ĵȷֵ㣬�������£�����1+2+3+4+5=15����㣮�߳�Ϊ1���������Σ���һ����1�����ڶ�����2������������3�������IJ���4��������1+2+3+4=10�����߶���Ϊ3��10=30�����߳�Ϊ2������������1+2+3=6�����߶���Ϊ3��6=18�����߳�Ϊ3������������3�����߶���Ϊ3��3=9���߳�Ϊ4������������1�����߶���Ϊ3�����ܹ���3��(1+2+3+4+1+2+3+3+1)=4��(1+2+3+4+5)=60���߶Σ�
��������α��ʷֵ������еĽ�����Ϊ10�����߶���Ϊ60����
��������̽����һ���߳�Ϊn(n��2)���������ε�������n�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬�������£�����1+2+3+4+5+��n=![]() ����㣮�߳�Ϊ1���������Σ���һ����1�����ڶ�����2������������3�������IJ���4������n����n��������(1+2+3+4+��+n)�����߶���Ϊ3��(1+2+3+4+��+n)�����߳�Ϊ2������������1+2+3=6�����߶���Ϊ3��6=18�����߳�Ϊ3������������3�����߶���Ϊ3��3=9���߳�Ϊ4������������1�����߶���Ϊ3�������߳�Ϊn��������1�����߶���Ϊ3���ܹ���n(1+2+3+��+n+1)=
����㣮�߳�Ϊ1���������Σ���һ����1�����ڶ�����2������������3�������IJ���4������n����n��������(1+2+3+4+��+n)�����߶���Ϊ3��(1+2+3+4+��+n)�����߳�Ϊ2������������1+2+3=6�����߶���Ϊ3��6=18�����߳�Ϊ3������������3�����߶���Ϊ3��3=9���߳�Ϊ4������������1�����߶���Ϊ3�������߳�Ϊn��������1�����߶���Ϊ3���ܹ���n(1+2+3+��+n+1)=![]() ��
��
��������α��ʷֵ������еĽ�����Ϊ![]() �����߶���Ϊ
�����߶���Ϊ![]() ����
����
ʵ��Ӧ�ã���һ���߳�Ϊ30���������ε���������ʮ�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬��������α��ʷֵ������еĽ�����Ϊ![]() =465�����������߶�����=
=465�����������߶�����=![]() =14880���߶Σ�
=14880���߶Σ�
�������α��ʷֵ������еĽ�����Ϊ465�����߶���Ϊ14880����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ά��������Ȩ�ͺ���Ȩ�������ಿ�Ŷ��ҹ��캣ʵ���˳�̬��Ѳ����������ͼ������ִ��Ѳ������ĺ��ബ��ÿСʱ50������ٶ������������У���![]() ����õ���
����õ���![]() �ڱ�ƫ��
�ڱ�ƫ��![]() �����ϣ���������1Сʱ����
�����ϣ���������1Сʱ����![]() ������ʱ��õ���
������ʱ��õ���![]() �ڱ�ƫ��
�ڱ�ƫ��![]() �����ϣ�
�����ϣ�
��1����![]() �Ķ�����
�Ķ�����
��2����֪�ڵ���![]() ����Χ25�������а������ʺ��ബ�����������������Ƿ�ȫ��
����Χ25�������а������ʺ��ബ�����������������Ƿ�ȫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD �ı߳�Ϊ4��E ΪAB ��һ�㣬��AE=3 ��F ΪBC ���ϵ�һ�����㣬����EF ����EF Ϊ�������������ֱ��������FEG ��EG=EF����GEF=90��������AG ����AG ����СֵΪ________________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������y=![]() x2+bx+c��x�ύ��A(-1��0)��B���㣨A��B��y�ύ�ڵ�C��0��-3����
x2+bx+c��x�ύ��A(-1��0)��B���㣨A��B��y�ύ�ڵ�C��0��-3����
��1���������ߵĽ���ʽ��
��2������D���߶�BC�·��������ϵĶ��㣬���ı���ABCD��������ֵ��
��3������E��x���ϣ���P���������ϣ��Ƿ������B��C��E��PΪ��������BCΪһ�ߵ�ƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
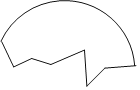
����Ŀ������ѧ�ҷ�����һ��Ŵ�Բ��������Ƭ��ͼ��ʾ��Ϊ�������������Ƭ����Ҫ�ҳ�Բ�ģ�
��1�������ó߹���ͼȷ������Ƭ��Բ��O����������ͼ�ۼ�����д������
��2��д����ͼ����Ҫ���ݣ�_______________________________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������±��ش����⣺
x | 16 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 175.56 | 278.89 | 282.24 |
��1��272.25��ƽ������������������
��2��![]() =��������������
=�������������� ![]() =��������������
=�������������� ![]() =������������
=������������
��3����![]() ����������Ϊa����4a����������
����������Ϊa����4a����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з������Ӧ���⣺
���조һ��һ·�����ʺ����߷���̳�ٰ�֮��ij�����������ס���������Ʒ��8���������һ��һ·�����߹��Һ͵�������֪3��������Ʒ��5��������Ʒ������������ͬ��2��������Ʒ��3��������Ʒ�����������200Ԫ. �ʼס���������Ʒ�����۵��۷ֱ��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ���꼶ѧ���������б�����ȫ�꼶ѧ�����μӣ�ѧУ�Ա��������ѧ�����б��ã�����һ���������Ƚ������������ĸ���������꼶��1����Ļ�������Ƴ���ͼ��ʾ��������������ͳ��ͼ�������ͼ�е���Ϣ������������⣺

��1�����꼶��1����� ��ѧ����
��2��������ͼ����������������ͳ��ͼ�У������Ƚ�����Ӧ�����ε�Բ�ĽǶ����� ��
��3������þ��꼶����1250��ѧ����������ٻ�һ���������Ƚ���ѧ�����ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ�κ���y��kx+b��ͼ���뷴��������y��![]() ��ͼ����M��N���㣮
��ͼ����M��N���㣮
��1������ͼ���������������������һ�κ����Ľ���ʽ��
��2������OM��ON������MON�������
��3������ͼ��ֱ��д��ʹһ�κ�����ֵ���ڷ�����������ֵ��x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com