
【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于M、N两点.
的图象交于M、N两点.
(1)根据图中条件求出反比例函数和一次函数的解析式;
(2)连结OM、ON,求△MON的面积;
(3)根据图象,直接写出使一次函数的值大于反比例函数的值的x的取值范围.

【答案】(1)y=2x﹣4.(2)8,(3)﹣1<x<0或x>3
【解析】
(1)把M(3,2)代入y=![]() ,即可求得m,得到y=
,即可求得m,得到y=![]() ,代入N(﹣1,a)求得a,得到N(﹣1,﹣6),把两点代入y=kx+b,解之即可求得k、b,从而求出两函数的解析式;
,代入N(﹣1,a)求得a,得到N(﹣1,﹣6),把两点代入y=kx+b,解之即可求得k、b,从而求出两函数的解析式;
(2)设直线MN交x轴于点A,求得A点坐标,然后根据S△MON=S△MOA+S△NOA求得即可;
(3)根据M,N的坐标即可得到结论.
解:(1)∵一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于M(3,2)、N(﹣1,a)两点
的图象交于M(3,2)、N(﹣1,a)两点
∴m=6,a=﹣6,
∴反比例函数y=![]() ,N(﹣1,﹣6),
,N(﹣1,﹣6),
把M(3,2),N(﹣1,﹣6)代入y=kx+b得![]() ,
,
解得![]() ,
,
∴一次函数的解析式的解析式为y=2x﹣4.
(2)设直线MN交x轴于点A,
当y=0时,2x﹣4=0,
∴x=2,
∴A(2,0),
∴S△MON=S△MOA+S△NOA=![]() OA(yM﹣yN)=
OA(yM﹣yN)=![]() ×2×8=8;
×2×8=8;
(3)由图象可知,当﹣1<x<0或x>3时一次函数的值大于反比例函数的值.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】问题提出:将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点, 则该三角形被剖分的网格中的结点个数和线段数分别是多少呢?
问题探究:要研究上面的问题,我们不妨先从特例入手,进而找到一般规律
探究一:将一个边长为2的正三角形的三条边平分,连接各边中点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?
如图1,连接边长为2的正三角形三条边的中点,从上往下:共有1+2+3=6个结点.边长为1的正三角形,第一层有1个,第二层有2个,共有1+2=3个,线段数为3×3=9条;边长为2的正三角形有1个,线段数为3条,总共有3×(1+2+1)=2×(1+2+3)=12条线段.

探究二:将一个边长为3的正三角形的三条边三等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?
如图2,连接边长为3的正三角形三条边的对应三等分点,从上往下:共有1+2+3+4=10个结点.边长为1的正三角形,第一层有1个,第二层有2个,第三层有3个,共有1+2+3=6个,线段数为3×6=18条;边长为2的正三角形有1+2=3个,线段数为3×3=9条,边长为3的正三角形有1个,线段数为3条,总共有3×(1+2+3+1+2+1)=3×(1+2+3+4)=30条线段.
探究三:
请你仿照上面的方法,探究将边长为4的正三角形的三条边四等分(图3),连接各边对应的等分点,该三角形被剖分的网格中的结点个数和线段数分别是多少?
(画出示意图,并写出探究过程)
问题解决:
请你仿照上面的方法,探究将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?(写出探究过程)
实际应用:
将一个边长为30的正三角形的三条边三十等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线l1、l2,直线l3和直线l1、l2交于点C和D,在直线l3上有动点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
(1)如果点P在C、D之间运动时,且满足∠1+∠3=∠2,请写出l1与l2之间的位置关系 ;
(2)如图②如果l1∥l2,点P在直线l1的上方运动时,试猜想∠1+∠2与∠3之间关系并给予证明;
(3)如果l1∥l2,点P在直线l2的下方运动时,请直接写出∠PAC、∠PBD、∠APB之间的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将两张正方形纸片A与三张正方形纸片B放在一起(不重叠无缝隙),拼成一个宽为10的长方形,求正方形纸片A、B的边长.
(2)如图2,将一张正方形纸片D放在一正方形纸片C的内部,阴影部分的面积为4;如图3,将正方形纸片C、D各一张并列放置后构造一个新的正方形,阴影部分的面积为48,求正方形C、D的面积之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图, 请根据图中提供的信息,完成下列问题:
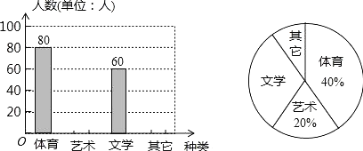
(1)此次共调查了 人;
(2)求文学社团在扇形统计图中所占圆心角为 度;
(3)请将条形统计图补充完整;
(4)若该校有 1500 名学生,请估计喜欢体育类社团的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副含30°和45°角的三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm(如图1),点G为边BC(EF)的中点,边FD与AB相交于点H,此时线段BH的长是____.现将三角板DEF绕点G按顺时针方向旋转(如图2),在∠CGF从0°到60°的变化过程中,点H相应移动的路径长共为_________.(结果保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com