
【题目】一副含30°和45°角的三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm(如图1),点G为边BC(EF)的中点,边FD与AB相交于点H,此时线段BH的长是____.现将三角板DEF绕点G按顺时针方向旋转(如图2),在∠CGF从0°到60°的变化过程中,点H相应移动的路径长共为_________.(结果保留根号).

【答案】 12![]() -12 12
-12 12![]() -18
-18
【解析】解:如图1中,作HM⊥BC于M,设HM=a,则CM=HM=a.
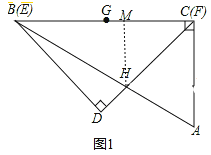
在Rt△ABC中,∠ABC=30°,BC=12,在Rt△BHM中,BH=2HM=2a,BM=![]() a,∵BM+FM=BC,∴
a,∵BM+FM=BC,∴![]() a+a=12,∴a=6
a+a=12,∴a=6![]() ﹣6,∴BH=2a=
﹣6,∴BH=2a=![]() .
.
如图2中,当DG⊥AB时,易证GH1⊥DF,此时BH1的值最小,易知BH1=BK+KH1=3![]() +3,
+3,
∴HH1=BH﹣BH1=9![]() ﹣15,当旋转角为60°时,F与H2重合,易知BH2=6
﹣15,当旋转角为60°时,F与H2重合,易知BH2=6![]() ,观察图象可知,在∠CGF从0°到60°的变化过程中,点H相应移动的路径长=2HH1+HH2=18
,观察图象可知,在∠CGF从0°到60°的变化过程中,点H相应移动的路径长=2HH1+HH2=18![]() ﹣30+[6
﹣30+[6![]() ﹣(12
﹣(12![]() ﹣12)]=
﹣12)]= ![]() .故答案为:
.故答案为: ![]() ,
, ![]() .
.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于M、N两点.
的图象交于M、N两点.
(1)根据图中条件求出反比例函数和一次函数的解析式;
(2)连结OM、ON,求△MON的面积;
(3)根据图象,直接写出使一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
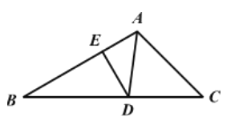
【题目】如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( )
A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上,且
上,且![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]()

(1)求证:![]() .
.
(2)判断![]() 的形状,并说明理由.
的形状,并说明理由.
(3)若![]() ,当
,当![]() _______时,
_______时,![]() .请说明理由.
.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙两人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min.求乙到达科技馆时,甲离科技馆还有多远.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.
计时制:0.05元/分;
包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.有下列结论;①A,B两城相距300 km;②小路的车比小带的车晚出发1 h,却早到1 h;③小路的车出发后2.5 h追上小带的车;④当小带和小路的车相距50 km时,t=![]() 或t=
或t=![]() .其中正确的结论有( )
.其中正确的结论有( )

A. ①②③④B. ①②④
C. ①②D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在平面直角坐标系中,作出下列各点,A(-3,4), B(-3,-2),O(0,0),并把各点连起来.
(2)画出△ABO先向下平移2个单位,再向右平移4 个单位得到的图形△A1B1o1,并直接写出A1坐标
(3) 直接写出三角形ABO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形EFGH是矩形ABCD的内接矩形,且EF:FG=3:1,AB:BC=2:1,则tan∠AHE的值为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com