
【题目】如图①,已知直线l1、l2,直线l3和直线l1、l2交于点C和D,在直线l3上有动点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
(1)如果点P在C、D之间运动时,且满足∠1+∠3=∠2,请写出l1与l2之间的位置关系 ;
(2)如图②如果l1∥l2,点P在直线l1的上方运动时,试猜想∠1+∠2与∠3之间关系并给予证明;
(3)如果l1∥l2,点P在直线l2的下方运动时,请直接写出∠PAC、∠PBD、∠APB之间的关系.

【答案】(1)l1∥l2;(2)∠1+∠2=∠3;理由见解析;(3)∠APB+∠PBD=∠PAC.
【解析】
(1)延长BP交AC于E,则∠2为△APE的外角,所以∠2=∠1+∠AEP,又因为∠2=∠1+∠3,等量代换∠3=∠AEP,根据内错角相等两直线平行,可知l1∥l2,(2)同(1)利用三角形的外角性质及平行线的性质可得∠1+∠2=∠3,(3)过点P作PF∥l1,根据平行于同一条直线的两直线平行,可得PF∥l2,再由平行线的性质进而可得∠APB+∠PBD=∠PAC.
证明:(1)l1∥l2.理由如下,
如图①,延长BP交AC于E,
∵∠2=∠1+∠3,∠2=∠1+∠AEP,
∴∠3=∠AEP,
∴l1∥l2,

故答案为:l1∥l2.
(2)如图②所示,当点P在线段DC的延长线上时,∠1+∠2=∠3,
理由是:∵l1∥l2,
∴∠CEP=∠3
∵∠CEP=∠1+∠2,
∴∠1+∠2=∠3.

(3)如图③所示,当点P在直线l2的下方运动时,∠APB+∠PBD=∠PAC.
理由:过点P作PF∥l1,
∠FPA=∠1.
∵l1∥l2,
∴PF∥l2,
∴∠FPB=∠3,
∴∠FPA=∠2+∠FPB=∠2+∠3.
即∠APB+∠PBD=∠PAC.



 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
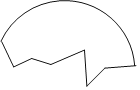
【题目】考古学家发现了一块古代圆形陶器残片如图所示,为了修复这块陶器残片,需要找出圆心.
(1)请利用尺规作图确定这块残片的圆心O;(保留作图痕迹,不写作法)
(2)写出作图的主要依据:_______________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为12 ,点B在点A右边,且OA2OB.
(1)写出数轴上点 B 表示的数;
(2)点 M 为数轴上一点,若 AM BM 4 ,求出点 M 表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知F是平行四边形ABCD的边DC中点,若三角形EFC,ABE,AFD的面积分别为3平方厘米,4平方厘米,5平方厘米,平行四边形ABCD的面积是整数。则三角形AEF的面积为_________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某品牌的饮料有大瓶与小瓶装之分.某超市花了2100元购进一批该品牌的饮料共800瓶,其中,大瓶和小瓶饮料的进价及售价如右表所示.
大瓶 | 小瓶 | |
进价(元/瓶) |
|
|
售价(元/瓶) |
|
|
(1)问:该超市购进大瓶和小瓶饮料各多少瓶?
(2)当大瓶饮料售出了200瓶,小瓶饮料售出了100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.请问:超市要使这批饮料售完后获得的利润为1075元,那么小瓶饮料作为赠品送出多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于M、N两点.
的图象交于M、N两点.
(1)根据图中条件求出反比例函数和一次函数的解析式;
(2)连结OM、ON,求△MON的面积;
(3)根据图象,直接写出使一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是长方形,∠A=∠ABC=∠BCD=∠CDA=90°,AB∥CD,AD∥BC,E是边AD上一动点.
(1)若∠ECD=2∠ECB,求∠AEC的度数.
(2)若∠ABD=70°,△DEF是等腰三角形,求∠ECB的度数.
(3)若△EFD的面积为4,若△DCF的面积为6,则四边形ABFE的面积为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,将一张矩形纸片 ABCD 沿着对角线 BD 向上折叠,顶点 C 落到点 E 处,BE 交 AD 于点 F.
(1)求证:△BDF 是等腰三角形;
(2)如图 2,过点 D 作 DG∥BE,交 BC 于点 G,连接 FG 交 BD 于点 O.
①判断四边形 BFDG 的形状,并说明理由;
②若 AB=6,AD=8,则 FG 的长为_____.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙两人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min.求乙到达科技馆时,甲离科技馆还有多远.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com