
【题目】(1)如图1,将两张正方形纸片A与三张正方形纸片B放在一起(不重叠无缝隙),拼成一个宽为10的长方形,求正方形纸片A、B的边长.
(2)如图2,将一张正方形纸片D放在一正方形纸片C的内部,阴影部分的面积为4;如图3,将正方形纸片C、D各一张并列放置后构造一个新的正方形,阴影部分的面积为48,求正方形C、D的面积之和.

【答案】(1)A、B的边长分别为4和6;(2)52.
【解析】
(1)设正方形A、B的边长分别为a、b,由题意得:正方形a的边长+正方形B的边长=10,2个正方形A的边长=3个正方形B的边长,根据等量关系列出方程组,再解即可;
(2)设正方形C、D的边长为c、d,由图2得:(c-d)2=4,由图3得:(c+d)2-c2-d2=48,然后两个方程组合可得c2+d2的值.
(1)设正方形A、B的边长分别为a、b,由题意得:![]() ,
,
解得:![]() ,
,
答:正方形A、B的边长分别为6,4;
(2)设正方形C、D的边长为c、d,则:
由图2得:(c-d)2=4,即:c2-2cd+d2=4,
由图3得:(c+d)2-c2-d2=48,即2dc=48,
∴c2+d2-48=4,
∴c2+d2=52,
即正方形C、D的面积和为52.


科目:初中数学 来源: 题型:
【题目】根据下表回答问题:
x | 16 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 175.56 | 278.89 | 282.24 |
(1)272.25的平方根是
(2)![]() = ,
= , ![]() = ,
= , ![]() =
=
(3)设![]() 的整数部分为a,求﹣4a的立方根.
的整数部分为a,求﹣4a的立方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,△ABC是等腰直角三角形,∠ACB=90°,正方形CDEF的顶点D、F分别在边AC、BC上,易证:AD=BF(不需要证明);
探究:将图①的正方形CDEF绕点C顺时针旋转α(0°<α<90°),连接AD、BF,其他条件不变,如图②,求证:AD=BF;
应用:若α=45°,CD=![]() ,BE=1,如图③,则BF= .
,BE=1,如图③,则BF= .
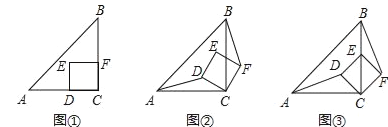
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出P点的坐标,若不存在说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于M、N两点.
的图象交于M、N两点.
(1)根据图中条件求出反比例函数和一次函数的解析式;
(2)连结OM、ON,求△MON的面积;
(3)根据图象,直接写出使一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 为
为![]() 上一动点,
上一动点,![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,下列有四个结论:①
,下列有四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 的周长为定值,其中正确的结论有( ).
的周长为定值,其中正确的结论有( ).

A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=x+4的图象与二次函数y=ax(x﹣2)的图象相交于A(﹣1,b)和B,点P是线段AB上的动点(不与A、B重合),过点P作PC⊥x轴,与二次函数y=ax(x﹣2)的图象交于点C.
(1)求a、b的值及B点的坐标;
(2)求线段PC长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.

(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,求∠AOC的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.
计时制:0.05元/分;
包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com