练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

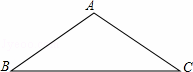
    如图，在△ABC中，

    （1）作△ABC的外接圆（只需作出图形，并保留作图痕迹）；

    （2）若△ABC是直角三角形，两直角边分别为6，8，求它的 外接圆半径．

     


    略（要求痕迹清楚）外接圆半径为5


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图所示，已知a∥b,AD⊥直线a,,求∠A的度数。

                                                                          

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在Rt△中，斜边上的高，，则________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在2×2的正方形网格中有9个格点，已经取定点A和B，在余下的7个点中任取一点C，使△ABC为等腰三角形的概率是（　 　）

    　   A．                       B．                              C．                            D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知点A(－2，y1)， B(，y2) 在二次函数的图象上，则 y1        y2(填“>”、“＝”或 “<”)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某大学生自主创业，在网上销售一种新上市的玩具，进价为20元。试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件。

     （1）写出销售这种玩具每天所得的销售利润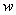（元）与销售单价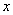（元）之间的函数关系式

    （2）求销售单价为多少元时，该玩具每天的销售利润最大。

    （3）该大学生结合上述情况，提出了A、B两种营销方案。

          方案A：该玩具的销售单价高于进价且不超过30元；

          方案B：每天销售量不少于10件，且每件玩具的利润至少为25元。

          请判断哪种方案的最大利润更高，并说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，⊙O的直径CD垂直弦AB于点E，且CE=2，DE=8，则AB的长为（   ）

    A．2             B．4              C．6               D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系xOy中，已知点M0的坐标为（1，0），将线段OM0绕原点O逆时针方向旋转45°，再将其延长到M1，使得M1M0⊥OM0，得到线段OM1；又将线段OM1绕原点O逆时针方向旋转45°，再将其延长到M2，使得M2M1⊥OM1，得到线段OM2；如此下去，得到线段OM3，OM4，OM5，…

    根据以上规律，请直接写出OM2014的长度为        ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


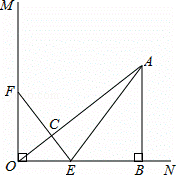
    如图，已知∠MON=90°，A是∠MON内部的一点，过点A作AB⊥ON，垂足为点B，AB=3厘米，OB=4厘米，动点E，F同时从O点出发，点E以1.5厘米/秒的速度沿ON方向运动，点F以2厘米/秒的速度沿OM方向运动，EF与OA交于点C，连接AE，当点E到达点B时，点F随之停止运动．设运动时间为t秒（t＞0）．

    （1）当t=1秒时，△EOF与△ABO是否相似？请说明理由；

    （2）在运动过程中，不论t取何值时，总有EF⊥OA．为什么？

    （3）连接AF，在运动过程中，是否存在某一时刻t，使得S△AEF=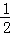S四边形ABOF？若存在，请求出此时t的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案