解:(1)设∠BAC=x°,则∠DAC=2x°,
∴∠ABC=∠ACB=

,
∠ABD=∠ADB=
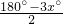
,
∠ACD=∠ADC=
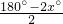
,
∴∠DBC=∠ABC-∠ABD,
=

-
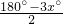
,
=x°,
∠BDC=∠ADC-∠ADB,
=
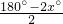
-
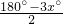
,
=

,
∴∠DBC/∠BDC=2;
(2)设∠BAC=x°,则∠DAC=3x°,
∴∠ABC=∠ACB=

,
∠ABD=∠ADB=
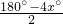
,
∠ACD=∠ADC=
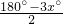
,
∴∠DBC=∠ABC-∠ABD,
=

-
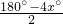
,
=
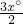
,
∠BDC=∠ADC-∠ADB,
=
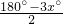
-
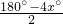
,
=

,
∴∠DBC/∠BDC=3;
(3)设∠BAC=x°,则∠DAC=nx°,
∴∠ABC=∠ACB=

,
∠ABD=∠ADB=
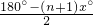
,
∠ACD=∠ADC=
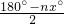
,
∴∠DBC=∠ABC-∠ABD,
=

-
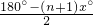
,
=
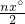
,
∠BDC=∠ADC-∠ADB,
=
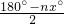
-
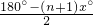
,
=

,
∴∠DBC/∠BDC=n.
故答案为:(1)2;(2)3;(3)n.
分析:(1)由题意,设∠BAC=x°,则∠DAC=2x°,∠DBC=∠ABC-∠ABD,∠BDC=∠ADC-∠ADB,根据三角形的内角和定理,可得∠ABC=∠ACB=

,∠ABD=∠ADB=
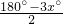
,∠ACD=∠ADC=
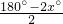
,代入即可求出;
(2)同理,当∠DAC=3∠BAC时,可求得∠DBC/∠BDC的值等于3;
(3)同理,当∠DAC=n∠BAC时,可求得∠DBC/∠BDC的值等于n.
点评:本题主要考查了等腰三角形的性质和三角形的内角和定理,由题意分别表示出各角的度数,是解答本题的关键.

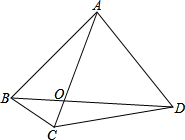 如图所示,已知四边形ABCD中,∠ABC=∠ACB,∠ABD=∠ADB,∠ACD=∠ADC,
如图所示,已知四边形ABCD中,∠ABC=∠ACB,∠ABD=∠ADB,∠ACD=∠ADC, ,
,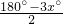 ,
,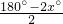 ,
, -
-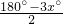 ,
,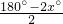 -
-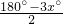 ,
, ,
, ,
,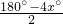 ,
,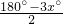 ,
, -
-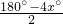 ,
,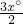 ,
,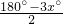 -
-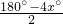 ,
, ,
, ,
,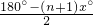 ,
,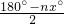 ,
, -
-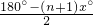 ,
,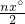 ,
,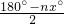 -
-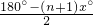 ,
, ,
, ,∠ABD=∠ADB=
,∠ABD=∠ADB=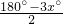 ,∠ACD=∠ADC=
,∠ACD=∠ADC=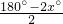 ,代入即可求出;
,代入即可求出;

 阅读快车系列答案
阅读快车系列答案 (2013•厦门)如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=
(2013•厦门)如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=
 如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=
如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=