
 如图正方形AOBC,等腰Rt△EOF中,∠EOF=90°,EF与OB交于G,连接AE、AB、BF.
如图正方形AOBC,等腰Rt△EOF中,∠EOF=90°,EF与OB交于G,连接AE、AB、BF. ,OE=3,求OG的长.
,OE=3,求OG的长. ,
, ,
, AB=
AB= ×5
×5 =5,
=5, =
= =4,
=4,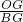 =
= =
= ,
,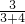 =
= .
.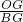 ,然后求解即可.
,然后求解即可.

科目:初中数学 来源: 题型:
| 2 |
| 2 |
 ,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.
,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
| k |
| x |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
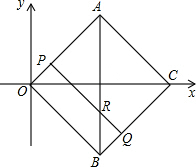
 ,0),动点P、Q同时从点O出发,点P沿着折线OACB的方向运动;点Q沿着折线OBCA的方向运动,设运动时间为t.
,0),动点P、Q同时从点O出发,点P沿着折线OACB的方向运动;点Q沿着折线OBCA的方向运动,设运动时间为t. 时,请求出直线PQ的解析式.
时,请求出直线PQ的解析式.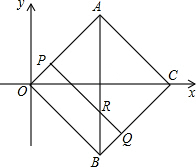 ,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.
,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.查看答案和解析>>
科目:初中数学 来源:2010年湖北省黄冈市黄州中学中考数学一模试卷(解析版) 题型:解答题
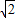 ,0),动点P、Q同时从点O出发,点P沿着折线OACB的方向运动;点Q沿着折线OBCA的方向运动,设运动时间为t.
,0),动点P、Q同时从点O出发,点P沿着折线OACB的方向运动;点Q沿着折线OBCA的方向运动,设运动时间为t.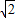 时,请求出直线PQ的解析式.
时,请求出直线PQ的解析式.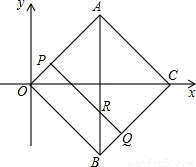
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com