
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A����Ϊ��2��4����ֱ��x=2��x���ཻ�ڵ�B������OA�����κ���y=x2ͼ��ӵ�O��OA����ƽ�ƣ���ֱ��x=2���ڵ�P������M��A��ʱֹͣ�ƶ���
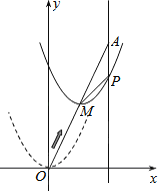
��1�����߶�OA����ֱ�ߵĺ�������ʽ��
��2������κ�������M�ĺ�����Ϊm����mΪ��ֵʱ���߶�PB��̣���������κ����ı���ʽ��
��3�����߶�PB���ʱ�����κ�����ͼ���Ƿ����Q��a��a��1������˵���ɣ�
���𰸡���1��y=2x����2��y=��x��1��2+2����3�����κ�����ͼ����Q��
��������
�����������1�����ݴ���ϵ������ü��ɣ�
��2����������õ�����M��m��2m��������ƽ�Ƶ����ʺͶ�������õ������ߵĽ���ʽΪy=��x��m��2+2m����x=2�������ʽ���P�������꣬�������PB=m2��2m+4=��m��1��2+3��0��m��2�������ݶ��κ��������ʵó���m=1ʱ��PB��̣�������õ�PB���ʱ�������ߵĽ���ʽΪy=��x��1��2+2��
��3�������κ�����ͼ���ǹ���Q��a��a��1�����������ʽ�õ�����a��1=��a��1��2+2����������0���˷����⣬˵���˶��κ�����ͼ����Q��
�⣺��1����ֱ��OA�Ľ���ʽΪy=kx��
��A��2��4����
��2k=4�����k=2��
���߶�OA����ֱ�ߵĺ�������ʽΪy=2x��
��2��������M�ĺ�����Ϊm������OA���ƶ���
��y=2m��0��m��2����
��M��m��2m����
�������ߵĽ���ʽΪy=��x��m��2+2m��
����x=2ʱ��y=��2��m��2+2m=m2��2m+4��0��m��2����
��PB=m2��2m+4=��m��1��2+3��0��m��2����
����m=1ʱ��PB��̣�
��PB���ʱ�������ߵĽ���ʽΪy=��x��1��2+2��
��3�������κ�����ͼ���ǹ���Q��a��a��1��
��a��1=��a��1��2+2�н⣮
������a2��3a+4=0�н⣬
�ߡ�=����3��2��4��1��4=��7��0��
�����κ�����ͼ����Q��


 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ������ƽ���ʽ������ǣ� ��
A. (a��b)(a��b) B. (��a��b)(��a��b) C. (��a+b)(a��b) D. (a��b)( ��a + b)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��̣�k��1��x2+��2k��3��x+k+1=0����������ȵ�ʵ����x1��x2��
��1����k��ȡֵ��Χ��
��2���Ƿ����ʵ��k��ʹ���̵���ʵ������Ϊ�෴����������ڣ����k��ֵ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���C��90�����ܳ�Ϊ60��б����һֱ�DZ߱���13��5����������������߳��ֱ��ǣ��� ��
A. 5��4��3 B. 13��12��5 C. 10��8��6 D. 26��24��10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A ( 5�� 3 ) �������Ϊ �� 3 �� -1�������A������������ͼ�α仯 �� ��
A .������ƽ��2����λ���ȣ�������ƽ��4����λ����
B. ������ƽ��2����λ���ȣ�������ƽ��4����λ����
C. ������ƽ��2����λ���ȣ�������ƽ��4����λ����
D. ������ƽ��2����λ���ȣ�������ƽ��4����λ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ε����߳��ֱ�Ϊ3��4��x����x�������ǣ� ��
A. 2 B. 4 C. 5 D. 8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������O��ֱ��Ϊ6���ף�Բ��O��ֱ��AB�ľ���Ϊ6���ף���ô��O��ֱ��AB��λ�ù�ϵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A������Ϊ����8��0����ֱ��BC������B����8��6����C��0��6�������ı���OABC�Ƶ�O��˳ʱ�뷽����ת�ǶȦ��õ��ı���OA��B��C�䣬��ʱ��OA�����BC���ڵ�P����B��C����BC���ӳ��߽��ڵ�Q������AP��
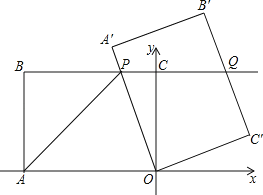
��1���ı���OABC����״�� ��
��2������ת�����У�����PAO=��POA����P�����꣮
��3������ת�����У���PΪ�߶�BQ�е�ʱ������OQ������OPQ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y=![]() ��ͼ����һ�κ���y=ax+b��ͼ���ཻ�ڵ�A��1��4���͵�B��n����2����
��ͼ����һ�κ���y=ax+b��ͼ���ཻ�ڵ�A��1��4���͵�B��n����2����
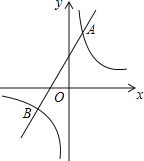
��1������������һ�κ����Ľ���ʽ��
��2����һ�κ�����ֵС�ڷ�����������ֵʱ��ֱ��д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com