【题目】如图，菱形ABCD的周长为8m，高AE的长为
cm，则对角线BD的长为（ ）
A．2cm B．3cm C．cm D．2cm
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案科目：初中数学 来源： 题型：
【题目】为响应国家的“节能减排”政策，某厂家开发了一种新型的电动车，如图，它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°，AT⊥MN，垂足为T，大灯照亮地面的宽度BC的长为
m．
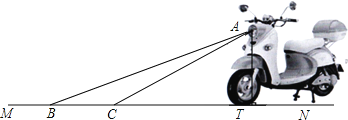
（1）求BT的长（不考虑其他因素）．
（2）一般正常人从发现危险到做出刹车动作的反应时间是0.2s，从发现危险到电动车完全停下所行驶的距离叫做最小安全距离．某人以20km/h的速度驾驶该车，从做出刹车动作到电动车停止的刹车距离是
，请判断该车大灯的设计是否能满足最小安全距离的要求（大灯与前轮前端间水平距离忽略不计），并说明理由．
（参考数据：sin22°≈
，tan22°≈
，sin31°≈
，tan31°≈
）
查看答案和解析>>
科目：初中数学 来源： 题型：
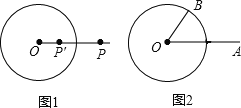
【题目】如图1，⊙O的半径为r（r＞0），若点P′在射线OP上，满足OP′OP=r2，则称点P′是点P关于⊙O的“反演点”．
如图2，⊙O的半径为4，点B在⊙O上，∠BOA=60°，OA=8，若点A′，B′分别是点A，B关于⊙O的反演点，求A′B′的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题满分6分）如图，已知AB∥DC，AE平分∠BAD，CD与AE相交于点F，∠CFE＝∠E．试说明AD∥BC．完成推理过程：
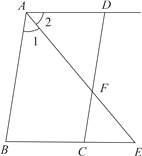
∵AB∥DC（已知）
∴∠1=∠CFE（ ）
∵AE平分∠BAD（已知）
∴∠1= ∠2 (角平分线的定义)
∵∠CFE=∠E(已知)∴∠2= （等量代换）
∴AD∥BC（ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB=3，BC=5，以B为圆心BC为半径画弧交AD于点E，如果点F是弧EC的中点，联结FB，那么tan∠FBC的值为 ．
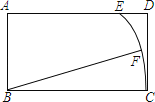
考点：全等三角形的判定与性质；角平分线的性质；矩形的性质；圆心角、弧、弦的关系；解直角三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
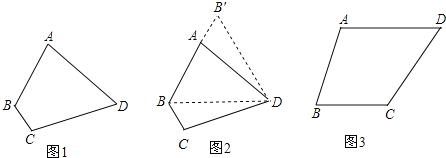
【题目】【问题提出】如图1，四边形ABCD中，AD=CD，∠ABC=120°，∠ADC=60°，AB=2，BC=1，求四边形ABCD的面积．
【尝试解决】
旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．
（1）如图2，连接 BD，由于AD=CD，所以可将△DCB绕点D顺时针方向旋转60°，得到△DAB′，则△BDB′的形状是 ．
（2）在（1）的基础上，求四边形ABCD的面积．
[类比应用]如图3，四边形ABCD中，AD=CD，∠ABC=75°，∠ADC=60°，AB=2，BC=
，求四边形ABCD的面积．
考点：几何变换综合题．
查看答案和解析>>
科目：初中数学 来源： 题型：
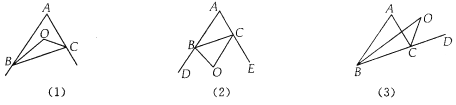
【题目】 在△ABC中，∠A＝40°．
（1）如图(1)BO、CO是△ABC的内角角平分线，且相交于点O，求∠BOC；
（2）如图(2)若BO、CO是△ABC的外角角平分线，且相交于点O，求∠BOC；
（3）如图(3)若BO、CO分别是△ABC的一内角和一外角角平分线，且相交于点O，求∠BOC；
（4）根据上述三问的结果，当∠A＝n°时，分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论)．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
