
【题目】【问题提出】如图1,四边形ABCD中,AD=CD,∠ABC=120°,∠ADC=60°,AB=2,BC=1,求四边形ABCD的面积.
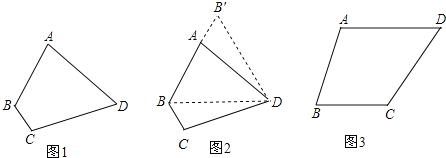
【尝试解决】
旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.
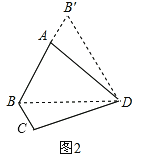
(1)如图2,连接 BD,由于AD=CD,所以可将△DCB绕点D顺时针方向旋转60°,得到△DAB′,则△BDB′的形状是 .
(2)在(1)的基础上,求四边形ABCD的面积.
[类比应用]如图3,四边形ABCD中,AD=CD,∠ABC=75°,∠ADC=60°,AB=2,BC=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
考点:几何变换综合题.
【答案】
【解析】
试题分析:(1)易证△DEB≌△DAB′,则BD=DB′,∠BDB′=60°,所以△BDB′是等边三角形;
(2)知等边三角形的边长为3,求出S△BDB′即可;
【类比应用】类比(1),连接 BD,由于AD=CD,所以可将△BCD绕点D逆时针方向旋转60°,得到△DAB′,连接BB′,延长BA,作B′E⊥BE;易证△AFB′是等腰直角三角形,△AEB是等腰直角三角形,利用勾股定理计算AE=B′E=1,BB′=![]() ,求△ABB′和△BDB′的面积和即可.
,求△ABB′和△BDB′的面积和即可.
解:(1)如图2,连接 BD,由于AD=CD,所以可将△DCB绕点D顺时针方向旋转60°,得到△DAB′,
∵BD=B′D,∠BDB′=60°
∴△BDB′是等边三角形;
(2)由(1)知,△BCD≌△B′AD,
∴四边形ABCD的面积=等边三角形BDB′的面积,
∵BC=AB′=1
∴BB′=AB+AB′=2+1=3,
∴S四边形ABCD=S△BDB′=![]() =
=![]() ;
;
【类比应用】如图3,连接 BD,由于AD=CD,所以可将△BCD绕点D逆时针方向旋转60°,得到△DAB′,
连接BB′,延长BA,作B′E⊥BE;
∵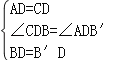 ,
,
∴△BCD≌△B′AD
∴S四边形ABCD=S四边形BDB′A,
∵∠ABC=75°,∠ADC=60°,
∴∠BAB′=135°
∴∠B′AE=45°,
∵B′A=BC=![]() ,
,
∴B′E=AE=1,
∴BE=AB+AE=2+1=3,
∴BB′=![]() ,
,
∴S△ABB′=![]() ABB′E=
ABB′E=![]() ×2×1=1,
×2×1=1,
S△BDB′=![]() =
=![]() ,
,
∴S四边形ABCD=S四边形BDB′A=S△BDB′﹣S△ABB′=![]() ﹣1.
﹣1.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:初中数学 来源: 题型:
【题目】以下列各组线段为边,能组成三角形的是( )
A. 3cm.4cm.8cm
B. 8cm,7cm,15cm
C. 5cm,5cm,11cm
D. 11cm,12cm,13crn
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
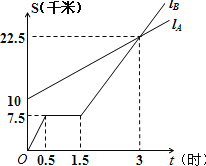
(1)B出发时与A相距 千米.
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com