
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
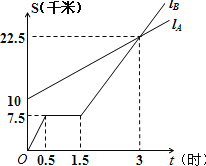
(1)B出发时与A相距 千米.
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
【答案】(1)10千米;(2)1小时(3)3小时(4)S=![]() t+10
t+10
【解析】
试题分析:(1)从图上可看出B出发时与A相距10千米.
(2)修理的时间就是路程不变的时间是1.5﹣0.5=1小时.
(3)从图象看出3小时时,两个图象相交,所以3小时时相遇.
(4)S和t的函数关系是一次函数,设函数是为S=kt+b,过(0,10)和(3,22.5),从而可求出关系式.
解:(1)由图形可得B出发时与A相距10千米;
(2)在图中发现0.5至1.5小时,自行车没有行走,
故可得出修理所用的时间为1小时.
(3)图中两直线的交点是B与A相遇的时刻,
即出发3小时后与A相遇.
(4)设函数是为S=kt+b,且过(0,10)和(3,22.5),
则![]() ,
,
解得:![]() .
.
故S与时间t的函数关系式为:S=![]() t+10.
t+10.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:
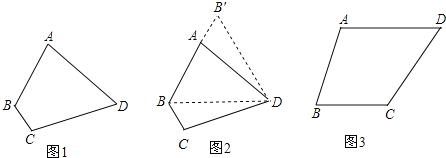
【题目】【问题提出】如图1,四边形ABCD中,AD=CD,∠ABC=120°,∠ADC=60°,AB=2,BC=1,求四边形ABCD的面积.
【尝试解决】
旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.
(1)如图2,连接 BD,由于AD=CD,所以可将△DCB绕点D顺时针方向旋转60°,得到△DAB′,则△BDB′的形状是 .
(2)在(1)的基础上,求四边形ABCD的面积.
[类比应用]如图3,四边形ABCD中,AD=CD,∠ABC=75°,∠ADC=60°,AB=2,BC=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
考点:几何变换综合题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 y=ax2+bx+c(a≠0)的图象经过点A(4,0),B(2,8),且以x=1为对称轴.
(1)求此函数的解析式,并作出它的示意图;
(2)当0<x<4时,写出y的取值范围;
(3)结合图象直接写出不等式ax2+bx+c>0(a≠0)的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】气象台预报“本市明天降水概率是30%”,对此消息下列说法正确的是( )
A.本市明天将有30%的地区降水
B.本市明天将有30%的时间降水
C.本市明天有可能降水
D.本市明天肯定不降水
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你对“0”有多少了解?下列关于“0”的说法错误的是( )
A. 任何数与0相乘都得0 B. 0是最小的有理数
C. 绝对值最小的有理数是0 D. 0没有倒数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com