
【题目】如图,直线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() ,
,![]() .
.

(1)若∠AOF=50°,求∠BOE的度数;
(2)若∠BOD:∠BOE=1:4,求∠AOF的度数.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据补角,余角的关系,可得∠COB,根据角平分线的定义,可得答案;
(2)根据邻补角,可得关于x的方程,根据解方程,可得∠AOC,再根据余角的定义,可得答案.
(1)∵∠COF与∠DOF是邻补角,
∴∠COF=180°∠DOF=90°.
∵∠AOC与∠AOF互为余角,
∴∠AOC=90°∠AOF=90°50°=40°.
∵∠AOC与∠BOC是邻补角,
∴∠COB=180°∠AOC=180°40°=140°.
∵OE平分∠BOC,
∴∠BOE=![]() ∠BOC=70°;
∠BOC=70°;
(2)∠BOD:∠BOE=1:4,
设∠BOD=∠AOC=x,∠BOE=∠COE=4x.
∵∠AOC与∠BOC是邻补角,
∴∠AOC+∠BOC=180°,
即x+4x+4x=180°,
解得x=20°.
∵∠AOC与∠AOF互为余角,
∴∠AOF=90°∠AOC=90°20°=70°.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】某家装公司聘请两队搬运工来搬运货物,他们都只能连续搬运5小时,甲队于某日0时开始搬运,过了1小时,乙队也开始搬运,如图,线段OG表示甲队搬运量y(千克)与时间x(时)的函数图象,线段EF表示乙队搬运量y(千克)与时间x(时)的函数图象.
(1)求乙队搬运量y与时间x之间的函数关系式.
(2)如果甲、乙两队各连续搬运5小时,那么乙队比甲队多搬运多少千克?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=___________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 的三条边长分别为6,8,12,过
的三条边长分别为6,8,12,过![]() 任一顶点画一条直线,将
任一顶点画一条直线,将![]() 分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
A.6条B.7条C.8条D.9条
查看答案和解析>>
科目:初中数学 来源: 题型:
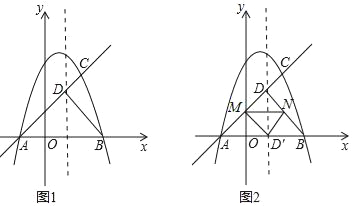
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点,(点A在点B的左侧),与直线AC交于点C(2,3),直线AC与抛物线的对称轴l相交于点D,连接BD.
(1)求抛物线的函数表达式,并求出点D的坐标;
(2)如图2,若点M、N同时从点D出发,均以每秒1个单位长度的速度分别沿DA、DB运动,连接MN,将△DMN沿MN翻折,得到△D′MN,判断四边形DMD′N的形状,并说明理由,当运动时间t为何值时,点D′恰好落在x轴上?
(3)在平面内,是否存在点P(异于A点),使得以P、B、D为顶点的三角形与△ABD相似(全等除外)?若存在,请直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣7.3)+5
(2)3﹣(﹣5)
(3)![]()
(4)(﹣12)÷(﹣![]() )
)
(5)4.7﹣(﹣8.9)﹣7.5+(﹣6)
(6)﹣3.5÷![]() ×|﹣
×|﹣![]() |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一小长假的某一天,亮亮全家上午![]() 时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )
时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )

A.景点离亮亮的家![]() 千米
千米
B.亮亮到家的时间为![]() 时
时
C.小汽车返程的速度为![]() 千米/时
千米/时
D.![]() 时至
时至![]() 时,小汽车匀速行驶
时,小汽车匀速行驶
查看答案和解析>>
科目:初中数学 来源: 题型:
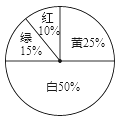
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(如下图),并规定:购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、绿、黄、白区域,那么顾客就可以分别得到80元、30元、10元、0元的购物券,凭购物券仍然可以在商场购物;如果顾客不愿意转转盘,那么可以直接获得购物券10元.
(1)每转动一次转盘所获购物券金额的平均数是多少?
(2)若在此商场购买100元的货物,那么你将选择哪种方式获得购物券?
(3)小明在家里也做了一个同样的转盘做实验,转10次后共获得购物券96元,他说还是不转转盘直接领取购物券合算,你同意小明的说法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:

(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com