练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    某中学篮球队8名队员的年龄情况如下：13、12、13、16、14、14、17、18，则这个队队员年龄的中位数是
     
    ．
    考点：中位数
    专题：
    分析：根据中位数的定义先把这组数据从小到大排列，找出最中间的数即可．
    解答：解：把这组数据从小到大排列为：12、13、13、14、14、16、17、18，最中间的数是14和14，
    则这个队队员年龄的中位数是（14+14）÷2=14；
    故答案为：14．
    点评：此题考查了中位数，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

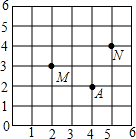    如图，若用（4，2）表示点A的位置，则表示点M，N的位置的有序数对分别是（　　）
    A、（2，3），（4，5）
    B、（2，3），（5，4）
    C、（3，2），（4，5）
    D、（3，2），（5，4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若点P（a，b）在第四象限的角平分线上，则a，b满足的关系是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    关于x的方程x+
    1
    2a-1
    =1    的解为x=2，则a的值为（　　）
    A、2
    B、1
    C、
    2
    3
    D、0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知矩形OABC的顶点O（0，0）、A（4，0）、B（4，3）．动点P从O出发，以每秒1个单位的速度，沿射线OB方向运动．设运动时间为t秒．
    （1）求P点的坐标（用含t的代数式表示）；
    （2）如图，以P为一顶点的正方形PQMN的边长为2，且边PQ⊥y轴．设正方形PQMN与矩形OABC的公共部分面积为S，当正方形PQMN与矩形OABC无公共部分时，运动停止．
    ①当t＜4时，求S与t之间的函数关系式；
    ②当t＞4时，设直线MQ、MN分别交矩形OABC的边BC、AB于D、E，问：是否存在这样的t，使得△PDE为直角三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一个自然数的立方，可以分裂成若干个连续奇数的和．例如：23，33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和，即23=3+5；33=7+9+11；43=13+15+17+19；…；若63也按照此规律来进行“分裂”，则63“分裂”出的奇数中，最大的奇数是（　　）
    A、37B、39C、41D、43

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在菱形ABCD中，AB=13cm，BC边上的高AH=5cm，那么对角线AC的长为
     
    cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，已知AB=AC=5，BC=6，△ABC按一定速度沿BC向右平移，平移后的三角形记为△DEF，平移距离不超过6（如图1），每到一个位置，都将△DEF绕E旋转，使DE始终经过点A，EF与AC交于点M（如图2）．

    （1）求证：△ABE∽△ECM；
    （2）若△AEM为等腰三角形，求△ABC平移的距离；
    （3）在平移和旋转的过程中，当线段AM最短时，求△AEM的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若一个三角形的周长是48，其中第一条边的长为3+2b，第二条边的长的2倍比第一条边的长少a-2b+2，求这个三角形第三条边的长．

    查看答案和解析>>

    同步练习册答案