
【题目】如图,已知OE,OF分别平分∠AOC,∠BOC,若∠EOF=45°,试判断OA与OB的位置关系,并说明理由. 
科目:初中数学 来源: 题型:
【题目】将一副三角尺(在RtΔABC中,∠ACB=90°,∠B=60°;在RtΔEDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将RtΔEDF绕点D顺时针方向旋转角α(0°<α<60°), DE交AC于点M,DF交BC于点N,则![]() 的值为( )
的值为( )
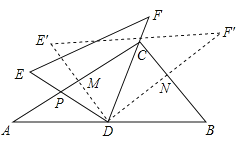
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)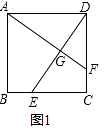
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;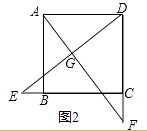
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.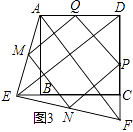
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月5日召开十三届全国人大二次会议,政府工作报告中提到2012年我国的贫困人口为9899万人,2018年减少到1660万人,连续6年平均每年减贫1300多万人,将数据1300万用科学记数法可表示为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程(组):
(1)![]()
(2)解二元一次方程组 ![]() 有位同学是这么做的,①+②得4x=20,解得x=5,代入①得y=﹣3.
有位同学是这么做的,①+②得4x=20,解得x=5,代入①得y=﹣3.
∴这个方程组的解为 ![]() .
.
该同学解这个二元一次方程组的过程中使用了消元法,目的是把二元一次方程组转化为求解;
(3)请你换一种方法来求解(2)中二元一次方程组.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF= ![]() ;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+
;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+ ![]() .其中正确的序号是(把你认为正确的都填上)
.其中正确的序号是(把你认为正确的都填上) 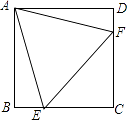
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com