Question

【题目】已知E，F分别为正方形ABCD的边BC，CD上的点，AF，DE相交于点G，当E，F分别为边BC，CD的中点时，有：①AF=DE；②AF⊥DE成立．
试探究下列问题：
（1）如图1，若点E不是边BC的中点，F不是边CD的中点，且CE=DF，上述结论①，②是否仍然成立？（请直接回答“成立”或“不成立”），不需要证明）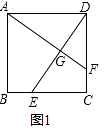

（2）如图2，若点E，F分别在CB的延长线和DC的延长线上，且CE=DF，此时，上述结论①，②是否仍然成立？若成立，请写出证明过程，若不成立，请说明理由；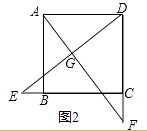

（3）如图3，在（2）的基础上，连接AE和EF，若点M，N，P，Q分别为AE，EF，FD，AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种，并证明你的结论．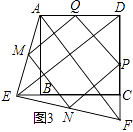

Answer 1

【答案】
（1）

解：上述结论①，②仍然成立，

理由为：∵四边形ABCD为正方形，

∴AD=DC，∠BCD=∠ADC=90°，

在△ADF和△DCE中，

，

∴△ADF≌△DCE（SAS），

∴AF=DE，∠DAF=∠CDE，

∵∠ADG+∠EDC=90°，

∴∠ADG+∠DAF=90°，

∴∠AGD=90°，即AF⊥DE

（2）

解：上述结论①，②仍然成立，

理由为：∵四边形ABCD为正方形，

∴AD=DC，∠BCD=∠ADC=90°，

在△ADF和△DCE中，

，

∴△ADF≌△DCE（SAS），

∴AF=DE，∠CDE=∠DAF，

∵∠ADG+∠EDC=90°，

∴∠ADG+∠DAF=90°，

∴∠AGD=90°，即AF⊥DE

（3）

解：四边形MNPQ是正方形．

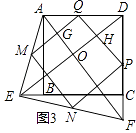
理由为：如图，设MQ，DE分别交AF于点G，O，PQ交DE于点H，

∵点M，N，P，Q分别为AE，EF，FD，AD的中点，

∴MQ=PN= DE，PQ=MN= AF，MQ∥DE，PQ∥AF，

∴四边形OHQG是平行四边形，

∵AF=DE，

∴MQ=PQ=PN=MN，

∴四边形MNPQ是菱形，

∵AF⊥DE，

∴∠AOD=90°，

∴∠HQG=∠AOD=90°，

∴四边形MNPQ是正方形．

【解析】（1）由四边形ABCD为正方形，CE=DF，易证得△ADF≌△DCE（SAS），即可证得AF=DE，∠DAF=∠CDE，又由∠ADG+∠EDC=90°，即可证得AF⊥DE；（2）由四边形ABCD为正方形，CE=DF，易证得△ADF≌△DCE（SAS），即可证得AF=DE，∠E=∠F，又由∠ADG+∠EDC=90°，即可证得AF⊥DE；（3）首先设MQ，DE分别交AF于点G，O，PQ交DE于点H，由点M，N，P，Q分别为AE，EF，FD，AD的中点，即可得MQ=PN= DE，PQ=MN= AF，MQ∥DE，PQ∥AF，然后由AF=DE，可证得四边形MNPQ是菱形，又由AF⊥DE即可证得四边形MNPQ是正方形．