
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F. 
(1)填空:∠AFC=度;
(2)求∠EDF的度数.
【答案】
(1)110
(2)解:∵∠B=50°,∠BAD=30°,
∴∠ADB=180°﹣50°﹣30°=100°,
∵△ABD沿AD折叠得到△AED,
∴∠ADE=∠ADB=100°,
∴∠EDF=∠EDA+∠BDA﹣∠BDF=100°+100°﹣180°=20°
【解析】解:(1)∵△ABD沿AD折叠得到△AED, ∴∠BAD=∠DAF,
∵∠B=50°∠BAD=30°,
∴∠AFC=∠B+∠BAD+∠DAF=110°;
故答案为110.
(1)根据折叠的特点得出∠BAD=∠DAF,再根据三角形一个外角等于它不相邻两个内角之和,即可得出答案;(2)根据已知求出∠ADB的值,再根据△ABD沿AD折叠得到△AED,得出∠ADE=∠ADB,最后根据∠EDF=∠EDA+∠BDA﹣∠BDF,即可得出答案.


科目:初中数学 来源: 题型:
【题目】利用电脑,在同一页面对某图形进行复制,得到一组图案,这一组图案可以看作一个基本图形通过( )得到的
A. 旋转 B. 平移和旋转
C. 平移 D. 拉伸
查看答案和解析>>
科目:初中数学 来源: 题型:
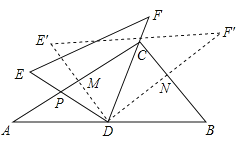
【题目】将一副三角尺(在RtΔABC中,∠ACB=90°,∠B=60°;在RtΔEDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将RtΔEDF绕点D顺时针方向旋转角α(0°<α<60°), DE交AC于点M,DF交BC于点N,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
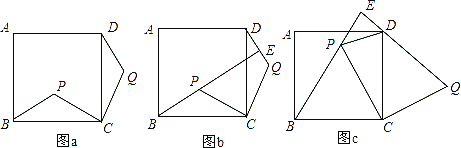
(1)、如图a,求证:△BCP≌△DCQ;
(2)、如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( ) 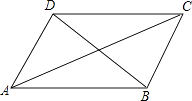
A.①②
B.②③
C.①③
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)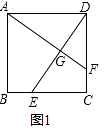
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;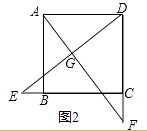
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.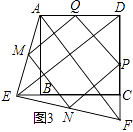
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程(组):
(1)![]()
(2)解二元一次方程组 ![]() 有位同学是这么做的,①+②得4x=20,解得x=5,代入①得y=﹣3.
有位同学是这么做的,①+②得4x=20,解得x=5,代入①得y=﹣3.
∴这个方程组的解为 ![]() .
.
该同学解这个二元一次方程组的过程中使用了消元法,目的是把二元一次方程组转化为求解;
(3)请你换一种方法来求解(2)中二元一次方程组.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com